
分析 先画出示意图,根据题意可求得∠PCB和∠PEC,转化为∠CPB,然后利用正弦定理求得BP,最后在Rt△BOP中求出OP即可.
解答 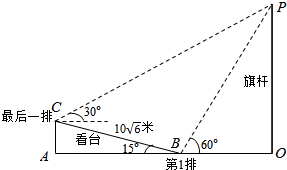 解:如图所示,依题意可知∠PCB=45°,
解:如图所示,依题意可知∠PCB=45°,
∠PEC=180°-60°-15°=105°
∴∠CPB=180°-45°-105°=30°
由正弦定理可知BP=$\frac{CB}{sin∠CPB}$•sin∠BCP=20$\sqrt{3}$米
∴在Rt△BOP中,
OP=PB•sin∠PBO=20$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=30米,
即旗杆的高度为30米.
点评 本题主要考查了解三角形的实际应用.此类问题的解决关键是建立数学模型,把实际问题转化成数学问题,利用正弦定理以及解三角形解答.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{e},\frac{{{e^2}+2}}{e})$ | B. | $(\frac{2}{e},+∞)$ | C. | $(\frac{1}{e},+∞)$ | D. | $(\frac{{{e^2}+2}}{e},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com