
工厂生产某种产品,次品率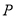 与日产量
与日产量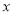 (万件)间的关系
(万件)间的关系 (
(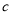 为常数,且
为常数,且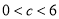 ),已知每生产一件合格产品盈利3元,每出现一件次品亏损1.5元
),已知每生产一件合格产品盈利3元,每出现一件次品亏损1.5元
(1)将日盈利额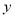 (万元)表示为日产量
(万元)表示为日产量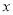 (万件)的函数;
(万件)的函数;
(2)为使日盈利额最大,日产量应为多少万件?(注: )
)
(1)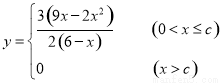 ;(2)当
;(2)当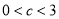 时,日产量为
时,日产量为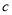 万件
万件 日盈利额最大;
日盈利额最大;
当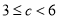 时,日产量为3万件时日盈利额最大.
时,日产量为3万件时日盈利额最大.
【解析】
试题分析:(1)要求日盈利额 (万元),只要找出日产量
(万元),只要找出日产量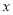 (万件)中正品与次品的数量,根据分段函数分段特征,针对不同的次品率得到不同的正品与次品数即可;(2)根据(1)分两段讨论函数的最大值:当
(万件)中正品与次品的数量,根据分段函数分段特征,针对不同的次品率得到不同的正品与次品数即可;(2)根据(1)分两段讨论函数的最大值:当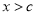 时,易知其日盈利额为0;当
时,易知其日盈利额为0;当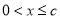 时,运用函数的导数在研究函数的单调性与最值中的应用,求出其最大值.最后综合两种情况写出所求结果即可.
时,运用函数的导数在研究函数的单调性与最值中的应用,求出其最大值.最后综合两种情况写出所求结果即可.
试题解析:(1)当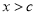 时,
时,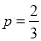 ,
,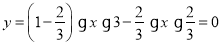
当 时,
时,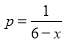
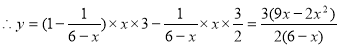
∴日盈利额 (万元)与日产量
(万元)与日产量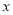 (万件)的函数关系式为
(万件)的函数关系式为
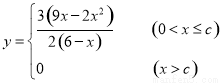 .
.
(2)当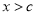 时,日盈利额为0;
时,日盈利额为0;
当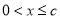 时,
时, ;
;
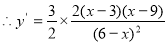 ,令
,令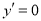 得
得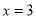 或
或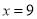 (舍去)
(舍去)
∴当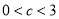 时,
时,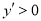
∴ 在
在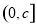 上单增
上单增
∴ 最大值
最大值 ;
;
当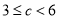 时,
时, 在
在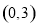 上单增,在
上单增,在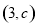 上单减
上单减
∴ 最大值
最大值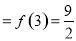 .
.
综上:当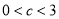 时,日产量为
时,日产量为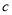 万件
万件 日盈利额最大;
日盈利额最大;
当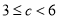 时,日产量为3万件时日盈利额最大.
时,日产量为3万件时日盈利额最大.
考点:分段函数的应用;导数在研究函数的单调性与最值中的应用.


科目:高中数学 来源:2015届湖南省娄底市名校高三9月联考文科数学试卷(解析版) 题型:选择题
已知角θ的顶点与原点重合,始边与x轴的正半轴重合,终边在直线y=2x上,则cos2θ=( )
A.- B.-
B.- C.
C.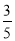 D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届湖北省高二上学期第一次月考理科数学试卷(解析版) 题型:选择题
已知 且
且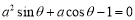 、
、 ,则连接
,则连接 、
、 两点的直线与单位圆
两点的直线与单位圆 的位置关系是( )
的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
查看答案和解析>>
科目:高中数学 来源:2015届湖北省高二上学期第一次月考理科数学试卷(解析版) 题型:选择题
下列关于随机抽样的说法不正确的是( )
A.简单随机抽样是一种逐个抽取不放回的抽样
B.系统抽样和分层抽样中每个个体被抽到的概率都相等
C.有2008个零件,先用随机数表法剔除8个,再用系统抽样方法抽取抽取20个作为样本,每个零件入选样本的概率都为
D.当总体是由差异明显的几个部分组成时适宜采取分层抽样
查看答案和解析>>
科目:高中数学 来源:2015届湖北省荆门市高二下学期期末质量检测理科数学试卷(解析版) 题型:填空题
若第一象限内的动点 满足
满足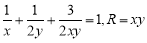 ,则以P为圆心,R为半径且面积最小的圆的方程为__ ___.
,则以P为圆心,R为半径且面积最小的圆的方程为__ ___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com