
分析 先利用同角三角函数的基本关系和二倍角公式化简整理tan$\frac{A+B}{2}$=sinC,得cos$\frac{A+B}{2}$=$\frac{\sqrt{2}}{2}$,进而求得A+B=90°.
对于①,tanA•cotB=tanA•tanA=1等式不一定成立;对于②,利用两角和公式化简,利用正弦函数的性质求得其范围符合,故②正确;对于③,sin2A+cos2B=2sin2A不一定等于1;④利用同角三角函数的基本关系可知cos2A+cos2B=cos2A+sin2A=1,根据C=90°可知sinC=1,故④正确.
解答 解:∵tan$\frac{A+B}{2}$=sinC,
∴$\frac{sin\frac{A+B}{2}}{cos\frac{A+B}{2}}$=2sin$\frac{A+B}{2}$cos$\frac{A+B}{2}$,
整理求得cos(A+B)=0,
∴A+B=90°.
∴$\frac{tanA}{tanB}$=tanA•cotB=tan2A,不一定等于1,故①不正确;
∴sinA+sinB=sinA+cosA=$\sqrt{2}$sin(A+45°),
45°<A+45°<135°,$\frac{\sqrt{2}}{2}$<sin(A+45°)≤1,
∴1<sinA+sinB≤$\sqrt{2}$,故②正确;
∵sin2A+cos2B=sin2A+sin2A=2sin2A=1不一定成立,故③不正确;
∵cos2A+cos2B=cos2A+sin2A=1,
sin2C=sin290°=1,
∴cos2A+cos2B=sin2C.故④正确.
综上知②④正确
故答案为:②④.
点评 本题考查命题的真假判断与应用,主要考查了三角函数的化简求值.考查了学生综合分析问题和推理的能力,考查了运算能力和转化思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | 5 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e | B. | 2e | C. | 3e | D. | 4e |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 赞成禁放 | 不赞成禁放 | 合计 | |
| 老年人 | 60 | 140 | 200 |
| 中青年人 | 80 | 120 | 200 |
| 合计 | 140 | 260 | 400 |
| P(k2>k0) | 0.050 | 0.025 | 0.010 |
| k0 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -8 | B. | -16 | C. | 55 | D. | 101 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
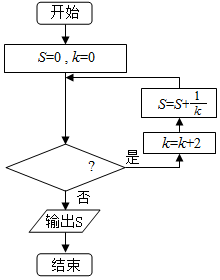
| A. | k≥7 | B. | k>7 | C. | k≤8 | D. | k<8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com