
分析 (I)求导数,据题意k=f′(1)=0,解得a值,再在定义域内解不等式f′(x)>0,f′(x)<0即可;
(II)f(x)的最大值大于1-$\frac{2}{a^2}$等价于lna2+a2<1,构造函数可判断a的取值范围;
解答 解:由已知有$f'(x)=\frac{1}{{{a^2}•x}}-1=\frac{{1-{a^2}•x}}{{{a^2}•x}}(x>0)$;
( I)因为f'(1)=0所以a2=1,即$f'(x)=\frac{1-x}{x}=0$得x=1;
因此函数f(x)的单调增区间为(0,1),单调减区间为(1,+∞).
( II)令f'(x)=0得$x=\frac{1}{a^2}({a^2}≠0)$,
则函数f(x)的在区间$(0,\frac{1}{a^2})$单调递增,在区间$(\frac{1}{a^2},+∞)$.单调递减;
即f(x)在$x=\frac{1}{a^2}$处取得最大值,最大值为$f(\frac{1}{a^2})=\frac{1}{a^2}ln\frac{1}{a^2}-\frac{1}{a^2}$;
因此f(x)的最大值大于1-$\frac{2}{a^2}$等价于lna2+a2<1…(*);
令t=a2(t>0),构造函数g(t)=lnt+t,则(*)式等价于g(t)=lnt+t<1;
因为函数g(t)=lnt+t在(0,+∞)为增函数且g(1)=1,
所以当0<t<1时有g(t)<1,当t>1时有g(t)>1;
即lna2+a2<1…(*)等价于0<a2<1即-1<a<0或0<a<1;
因此当f(x)的最大值大于1-$\frac{2}{a^2}$时,a的取值范围(-1,0)∪(0,1).
点评 本题考查利用导数研究函数单调性、曲线上某点切线方程,考查函数的最值求解,考查分类讨论思想,考查函数恒成立问题的解决,转化函数最值是解决恒成立问题的常用方法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
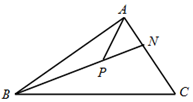 如图,在锐角△ABC中,$\overrightarrow{AN}$=$\frac{1}{2}$$\overrightarrow{NC}$,P是线段BN(不含端点)上的一点,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$,则$\frac{1}{m}$+$\frac{3}{n}$的最小值为16.
如图,在锐角△ABC中,$\overrightarrow{AN}$=$\frac{1}{2}$$\overrightarrow{NC}$,P是线段BN(不含端点)上的一点,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$,则$\frac{1}{m}$+$\frac{3}{n}$的最小值为16.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2-$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分接近π的实数的全体 | B. | 善良的人 | ||
| C. | A校高一(1)班所有聪明的学生 | D. | B单位所有身高在1.75 cm以上的人 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -8 | B. | -4 | C. | -2 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=xsinx | B. | y=$\frac{{e}^{x}+{e}^{-x}}{2}$ | C. | y=ln$\frac{1-x}{1+x}$ | D. | y=x3+x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{20}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com