
| 年级 | 相关教师数 | 抽取教师数 |
| 高一 | x | 4 |
| 高二 | 12 | 2 |
| 高三 | 18 | y |
分析 (Ⅰ)根据分层抽样的定义建立比例关系即可得到结论.
(Ⅱ)利用列举法,求出对应事件的个数,结合古典概型的概率公式进行计算即可.
解答 解:(Ⅰ)由分层抽样的定义得$\frac{4}{x}=\frac{2}{12}=\frac{y}{18}$得x=24,y=3,
(Ⅱ)高二抽取2人,设为A,B,高三抽取3人,设为a,b,c,从5人选2人有(A,B),(A,a),(A,b),(A,c),(B,a),(B,b),(B,c),
(a,b),(a,c),(b,c),共10种,若两位老师来自高三,则有(a,b),(a,c),(b,c),共3种,
则对应的概率P=$\frac{3}{10}$.
点评 本题主要考查分层抽样的应用以及古典概型的概率的计算,根据条件建立比例关系以及利用列举法是解决本题的关键.比较基础.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (-∞,1) | C. | (-1,+∞) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
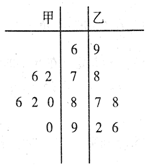 甲、乙两名学生的六次数学测试成绩(百分制)如图所示.
甲、乙两名学生的六次数学测试成绩(百分制)如图所示.| A. | ③④ | B. | ①② | C. | ②④ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{5}}{81}$π | B. | $\frac{4\sqrt{5}}{27}$π | C. | $\frac{4\sqrt{5}}{81}$π | D. | $\frac{\sqrt{10}}{81}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
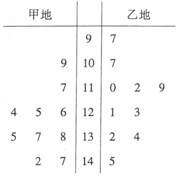 在一次期末模拟测试中,某市教研室在甲、乙两地各抽取了10名学生的数学成绩,得到茎叶图如图所示.
在一次期末模拟测试中,某市教研室在甲、乙两地各抽取了10名学生的数学成绩,得到茎叶图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | $\frac{{\sqrt{21}}}{3}$ | C. | $\frac{5}{4}$ | D. | $\frac{{\sqrt{7}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $3\sqrt{2}$ | C. | $\frac{3}{2}$ | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com