
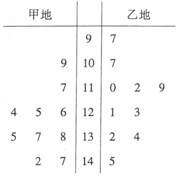
 在一次期末模拟测试中,某市教研室在甲、乙两地各抽取了10名学生的数学成绩,得到茎叶图如图所示.
在一次期末模拟测试中,某市教研室在甲、乙两地各抽取了10名学生的数学成绩,得到茎叶图如图所示.分析 (Ⅰ)由茎叶图能求出甲地抽取的10名学生的平均成绩和乙地抽取的10名学生的平均成绩.
(Ⅱ)从茎叶图可以看出:甲地学生成绩的极差比乙地学生的极差小,且甲地学生的成绩集中于[120,140]之间,乙地学生的成绩集中于[110,140]之间,由此能求出结果.
(Ⅲ)在甲地被抽取的10名学生中,从成绩在120分以上的8名学生中随机抽取2人,基本事件总数n=${C}_{8}^{2}$=28,利用列举法求出其中恰有1名学生成绩在140分以上包含的基本事件的个数,由此能求出恰有1名学生成绩在140分以上的概率.
解答 解:(Ⅰ)由茎叶图得甲地抽取的10名学生的平均成绩为:120+$\frac{1}{10}$(-11-3+4+5+6+15+17+18+22+27)=130,
乙地抽取的10名学生的平均成绩为:120+$\frac{1}{10}$(-23-13-10-8-1+1+3+12+14+25)=120.
(Ⅱ)从茎叶图可以看出:
甲地学生成绩的极差比乙地学生的极差小,且甲地学生的成绩集中于[120,140]之间,
乙地学生的成绩集中于[110,140]之间,
故甲地学生成绩较好.
(Ⅲ)在甲地被抽取的10名学生中,从成绩在120分以上的8名学生中随机抽取2人,
基本事件总数n=${C}_{8}^{2}$=28,
其中恰有1名学生成绩在140分以上包含的基本事件有:
(124,142),(124,147),(125,142),(125,147),(126,142),(126,147),
(135,142),(135,147),(137,142),(137,147),(138,142),(138,147),
共12个,
∴恰有1名学生成绩在140分以上的概率p=$\frac{12}{28}$=$\frac{3}{7}$.
点评 本题考查概率的求法,涉及到茎叶图、等可能事件概率计算公式、列举法等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想,是基础题.


 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 14 | B. | 13 | C. | 7 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年级 | 相关教师数 | 抽取教师数 |
| 高一 | x | 4 |
| 高二 | 12 | 2 |
| 高三 | 18 | y |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y=0 | B. | 2x+y-1=0 | C. | x-y=0 | D. | 2x-y-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
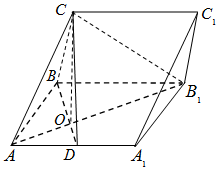 在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1.
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com