
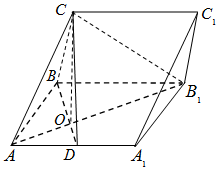
 在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1.
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1.分析 (Ⅰ)通过证明AB1⊥BD,AB1⊥CO,推出AB1⊥平面BCD,然后证明平面AB1C⊥平面BCD.
(Ⅱ)以O为坐标原点,分别以OD,OB1,OC所在直线为x,y,z轴,建立如图所示的空间直角坐标系O-xyz.求出平面ABC的法向量,设直线GD与平面ABC所成角α,利用空间向量的数量积求解直线GD与平面ABC所成角的正弦值即可.
解答 (本小题满分12分)
解:(Ⅰ)∵ABB1A1为矩形,AB=2,$A{A_1}=2\sqrt{2}$,D是AA1的中点,∴∠BAD=90°,$∠AB{B_1}={90^0}$,$B{B_1}=2\sqrt{2}$,$AD=\frac{1}{2}A{A_1}=\sqrt{2}$
从而$tan∠ABD=\frac{AD}{AB}=\frac{{\sqrt{2}}}{2}$,$tan∠A{B_1}B=\frac{AB}{{B{B_1}}}=\frac{{\sqrt{2}}}{2}$,∵$0<∠ABD,∠A{B_1}B<\frac{π}{2}$,∴∠ABD=∠AB1B,…(2分)
∴$∠A{B_1}B+∠BA{B_1}=∠ABD+∠BA{B_1}=\frac{π}{2}$,∴$∠AOB=\frac{π}{2}$,从而AB1⊥BD…(4分)
∵CO⊥平面ABB1A1,AB1?平面ABB1A1,∴AB1⊥CO,∵BD∩CO=O,∴AB1⊥平面BCD,
∵AB1?平面AB1C,
∴平面AB1C⊥平面BCD…(6分)
(Ⅱ)如图,以O为坐标原点,
分别以OD,OB1,OC所在直线为x,y,z轴,
建立如图所示的空间直角坐标系O-xyz.
在矩形ABB1A1中,由于AD∥BB1,所以△AOD和△B1OB相似,
从而$\frac{{O{B_1}}}{OA}=\frac{OB}{OD}=\frac{{B{B_1}}}{AD}=2$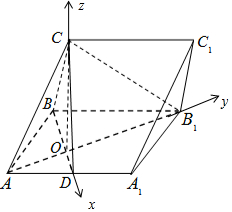
又$A{B_1}=\sqrt{A{A_1}^2+{A_1}{B_1}^2}=2\sqrt{3}$,$BD=\sqrt{A{D^2}+A{B^2}}=\sqrt{6}$∴$OB=\frac{{2\sqrt{6}}}{3}$,$OD=\frac{{\sqrt{6}}}{3}$,$OA=\frac{{2\sqrt{3}}}{3}$,$O{B_1}=\frac{{4\sqrt{3}}}{3}$,∴$A(0,-\frac{{2\sqrt{3}}}{3},0),B(-\frac{{2\sqrt{6}}}{3},0,0)$,$C(0,0,\frac{{2\sqrt{3}}}{3}),{B_1}(0,\frac{{4\sqrt{3}}}{3},0)$,$D(\frac{{\sqrt{6}}}{3},0,0)$∵G为△AB1C的重心,∴$G(0,\frac{{2\sqrt{3}}}{9},\frac{{2\sqrt{3}}}{9})$,$\overrightarrow{GD}=(\frac{{\sqrt{6}}}{3},-\frac{{2\sqrt{3}}}{9},-\frac{{2\sqrt{3}}}{9})$…(8分)
设平面ABC的法向量为$\overrightarrow n=(x,y,z)$,$\overrightarrow{AB}=(-\frac{{2\sqrt{6}}}{3},\frac{{2\sqrt{3}}}{3},0),\overrightarrow{AC}=(0,\frac{{2\sqrt{3}}}{3},\frac{{2\sqrt{3}}}{3})$,
由$\left\{{\begin{array}{l}{\overrightarrow n•\overrightarrow{AB}=0}\\{\overrightarrow n•\overrightarrow{AC}=0}\end{array}}\right.$可得$\left\{{\begin{array}{l}{-\frac{{2\sqrt{6}}}{3}x+\frac{{2\sqrt{3}}}{3}y=0}\\{\frac{{2\sqrt{3}}}{3}y+\frac{{2\sqrt{3}}}{3}z=0}\end{array}}\right.$$⇒\left\{{\begin{array}{l}{-\sqrt{2}x+y=0}\\{y+z=0}\end{array}}\right.$,
令y=1,则z=-1,$x=\frac{{\sqrt{2}}}{2}$,所以$\overrightarrow n=(\frac{{\sqrt{2}}}{2},1,-1)$.…(10分)
设直线GD与平面ABC所成角α,则$sinα=cos<\overrightarrow{GD},\overrightarrow n>=\frac{{\overrightarrow{GD}•\overrightarrow n}}{{|\overrightarrow{GD}|•|\overrightarrow n|}}=\frac{{(\frac{{\sqrt{6}}}{3},-\frac{{2\sqrt{3}}}{9},-\frac{{2\sqrt{3}}}{9})•(\frac{{\sqrt{2}}}{2},1,-1)}}{{\sqrt{\frac{26}{27}}×\frac{{\sqrt{10}}}{2}}}$=$\frac{{3\sqrt{65}}}{65}$,
所以直线GD与平面ABC所成角的正弦值为$\frac{{3\sqrt{65}}}{65}$…(12分)
点评 本题考查平面与平面垂直的判定定理的应用,直线与平面所成角的求法,考查空间想象能力以及计算能力.


科目:高中数学 来源: 题型:解答题
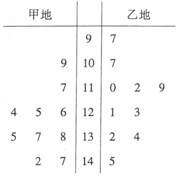 在一次期末模拟测试中,某市教研室在甲、乙两地各抽取了10名学生的数学成绩,得到茎叶图如图所示.
在一次期末模拟测试中,某市教研室在甲、乙两地各抽取了10名学生的数学成绩,得到茎叶图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $3\sqrt{2}$ | C. | $\frac{3}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | $[{-\sqrt{3},\sqrt{3}}]$ | C. | (-∞,-1]∪[1,+∞) | D. | [-$\sqrt{3}$,-1]∪[1,$\sqrt{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 2 | 3 | 4 | 5 | 6 |
| y | 25 | ● | 50 | 56 | 64 |
| A. | 37.4 | B. | 39 | C. | 38.5 | D. | 40.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>b>a | D. | a>c>b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com