
| A. | a>b>c | B. | b>a>c | C. | c>b>a | D. | a>c>b |
分析 根据题意得出$\frac{f{(x}_{1})}{{x}_{1}}$>$\frac{f{(x}_{2})}{{x}_{2}}$,构造函数g(x)=$\frac{f(x)}{x}$,则g(x)在(0,+∞)上是单调减函数;
变形a、b、c,比较它们的大小即可.
解答 解:函数f(x)是定义在R上的奇函数,
且对任意两个正数x1,x2(x1<x2),都有x2f(x1)>x1f(x2),
∴$\frac{f{(x}_{1})}{{x}_{1}}$>$\frac{f{(x}_{2})}{{x}_{2}}$;
设g(x)=$\frac{f(x)}{x}$,g(x)在(0,+∞)上是单调减函数;
又a=$\frac{1}{2}$f(2)=$\frac{f(2)}{2}$,
b=f(1)=$\frac{f(1)}{1}$,
c=-$\frac{1}{3}$f(-3)=$\frac{1}{3}$f(3)=$\frac{f(3)}{3}$,
∴g(1)>g(2)>g(3),
即b>a>c.
故选:B.
点评 本题考查了函数的奇偶性与单调性的应用问题,也考查了构造函数的应用问题,是中档题.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:解答题
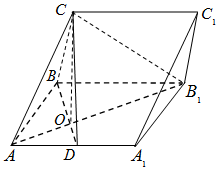 在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1.
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 不充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一个命题的逆命题为真,则它的逆否命题一定为真 | |
| B. | 若“ac2>bc2”,则a>b | |
| C. | ?x0∈R,$sin{x_0}+cos{x_0}=\frac{3}{2}$ | |
| D. | “a2+b2=0,则a,b全为0”的逆否命题是“若a,b全不为0,则a2+b2≠0” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com