
���� ��1���������У�2��3��6��m��m��6���ǡ��һ�ϵ����Ϊa�ġ��һ����С�����a-m��a-6��a-3��a-2Ҳ�Ǹ����е����a-m��a-6��a-3��a-2���ɴ˿���m��a��ֵ��
��2���ɡ��һ����С��Ķ���֤������{bn}�ǡ��һ����С�����֤������{bn}�е�����һ��bi��1��i��n0����a-bi=b1+��n0-i��d=bn0+1-i��{bn}���Ӷ���������{bn}������֮�ͣ�
��3��������������ĵȱ�����{cn}�������Ĺ���Ϊq��q��1������֪����{cn}��Ϊ�������У�����������Ϊn���ci+cn+1-i=a��1��i��n�����ٷ������ۣ����ɵõ����ۣ�
��� ��1���⣺��Ϊ2��3��6��m��m��6���ǡ��һ�ϵ����Ϊa�ġ��һ����С�
����a-m��a-6��a-3��a-2Ҳ�Ǹ����е����a-m��a-6��a-3��a-2��
��a-m=2��a-6=3����a=9��m=7��
��2��֤����������{bn}�Ĺ���Ϊd��
��Ϊ����{bn}������Ϊn0�������Ȳ�����
��b1��b2��b3�ܡ���b${\;}_{{n}_{0}}$����a-b1��a-b2��a-b3�ݡ���a-b${\;}_{{n}_{0}}$��
��������{bn}�е�����һ��bi��1��i��n0����a-bi=b1+��n0-i��d=b${\;}_{{n}_{0}}$+1-i��{bn}
ͬ���ɵã�b1��b2��b3�ݡ���b${\;}_{{n}_{0}}$��a-bi=b1+��n0-i��d=b${\;}_{{n}_{0}}$+1-i��{bn}Ҳ������
�ɡ��һ����С��Ķ����֪������{bn}�ǡ��һ����С���
����Ϊ����{bn}������֮����B������B=$\frac{��{b}_{1}+{b}_{{n}_{0}}��•{n}_{0}}{2}$=$\frac{a{n}_{0}}{2}$����a=$\frac{2B}{{n}_{0}}$��
��3���⣺������������ĵȱ�����{cn}�������Ĺ���Ϊq��q��1����
��Ϊ����{cn}Ϊ�������У�����c1��c2��c3������cn����a-c1��a-c2��a-c3������a-cn��
����Ϊ����{cn}Ϊ���һ����С�����a-ci��{cn}������a-ci��������
������{cn}��Ϊ�������У�����������Ϊn���ci+cn+1-i=a��1��i��n��
����n=3������c1+c3=a��c2=$\frac{a}{2}$����c22=c1c3���ɴ˵�q=1����q��1ì��
����n��4����c1+cn=c2+cn-1����c1-c1q+c1qn-1-c1qn-2=0
����q-1����1-qn-2��=0����q=1����q��1ì�ܣ�
�ۺϢ٢ڵã���������������������{cn}��
���� ���⿼���¶��壬����ѧ�����Ķ�����������ѧ�������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c | B�� | b��a��c | C�� | c��b��a | D�� | a��c��b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| P��K2��k0�� | 0.10 | 0.05 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
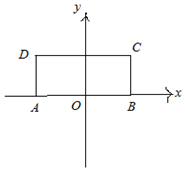 ��ͼ���ھ���ABCD�У�AB=12��BC=5����A��BΪ�����˫����$M��\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ǡ�ù�C��D���㣬��˫����M�ı�����Ϊ$\frac{x^2}{16}-\frac{y^2}{20}=1$��
��ͼ���ھ���ABCD�У�AB=12��BC=5����A��BΪ�����˫����$M��\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ǡ�ù�C��D���㣬��˫����M�ı�����Ϊ$\frac{x^2}{16}-\frac{y^2}{20}=1$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{25}{6}$ | B�� | $\frac{8}{3}$ | C�� | $\frac{11}{3}$ | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 0 | C�� | 2 | D�� | $2\sqrt{10}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �Vq | B�� | ���Vp���ţ��Vq�� | C�� | p��q | D�� | p�ģ��Vq�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com