
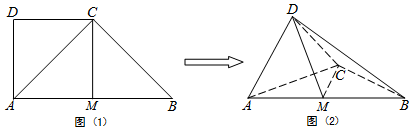
分析 (1)由已知求出AC,BC的长,利用勾股定理可得AC⊥BC,再由面面垂直的性质可得BC⊥平面ACD;
(2)由(1)知BC⊥平面ACD,然后利用等积法即可求得几何体D-ABC的体积.
解答 证明:(1)由图(1)可知,$AC=BC=2\sqrt{2}$,AB=4,
∴AC2+BC2=AB2,则AC⊥BC,
又∵平面ADC⊥平面ABC,平面ADC∩平面ABC=AC,BC?平面ABC,
∴BC⊥平面ACD;
解:(2)由(1)可知,BC⊥平面ACD,则BC即为几何体B-ACD的高,
∴${V_{D-ABC}}={V_{B-ACD}}=\frac{1}{3}{S_{△ACD}}•BC=\frac{1}{3}×(\frac{1}{2}×2×2)×2\sqrt{2}=\frac{4}{3}\sqrt{2}$.
点评 本题考查直线与平面垂直的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 不充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2016}{2017}$ | B. | $\frac{4032}{2017}$ | C. | $\frac{2017}{2018}$ | D. | $\frac{4034}{2018}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=9,则x=±3”的否命题为“若x2=9,则x≠±3” | |
| B. | 若命题P:?x0∈R,$x_0^2-3{x_0}-1>0$,则命题?P:?x∈R,$x_{\;}^2-3x-1<0$ | |
| C. | 设$\overrightarrow a,\overrightarrow b$是两个非零向量,则“$\overrightarrow a•\overrightarrow b<0$是“$\overrightarrow a,\overrightarrow b$夹角为钝角”的必要不充分条件 | |
| D. | 若命题P:$\frac{1}{x-2}>0$,则¬P:$\frac{1}{x-2}≤0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [10,+∞) | B. | [$\frac{29}{2}$,+∞) | C. | [$\frac{25}{2}$,+∞) | D. | [$\frac{41}{4}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com