
| A. | $\frac{2016}{2017}$ | B. | $\frac{4032}{2017}$ | C. | $\frac{2017}{2018}$ | D. | $\frac{4034}{2018}$ |
分析 数列{an}满足a1=1,且对于任意的n∈N*都有an+1=an+a1+n,可得an+1-an=1+n,利用an=a1+(a2-a1)+(a3-a2)+…+(an-an-1),可得an=$\frac{n(n+1)}{2}$.再利用裂项求和方法即可得出.
解答 解:∵数列{an}满足a1=1,且对于任意的n∈N*都有an+1=an+a1+n,
∴an+1-an=1+n,
∴an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=1+2+3+…+n
=$\frac{n(n+1)}{2}$.
∴$\frac{1}{{a}_{n}}$=$\frac{2}{n(n+1)}$=2$(\frac{1}{n}-\frac{1}{n+1})$.
∴$\frac{1}{a_1}+\frac{1}{a_2}+…+\frac{1}{{{a_{2017}}}}$=2$[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{2017}-\frac{1}{2018})]$
=2×$(1-\frac{1}{2018})$
=$\frac{2017}{1009}$=$\frac{4034}{2018}$.
故选:D.
点评 本题考查了数列递推关系、等差数列的通项公式与求和公式、累加求和方法、裂项求和方法,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
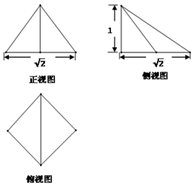 如图是一个简单几何体的三视图,则该几何体的体积为( )
如图是一个简单几何体的三视图,则该几何体的体积为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
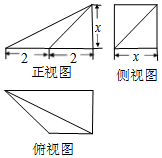
| A. | 3 | B. | 1 | C. | 2 | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
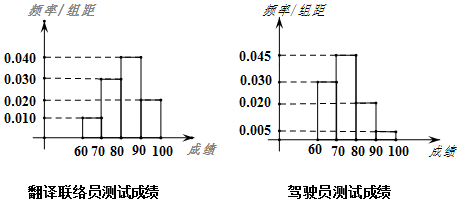
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
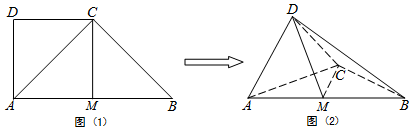
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>-2} | B. | {x|x>2} | C. | {x|0<x<2} | D. | {x|-2<x<2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com