
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 画出满足约束条件的可行域,求出目标函数的最大值,从而建立关于m的等式,即可得出答案.
解答 解:由z=x+my得y=-$\frac{1}{m}$x+$\frac{z}{m}$,
∵m>1,∴目标函数的斜率k=-$\frac{1}{m}$∈(-1,0),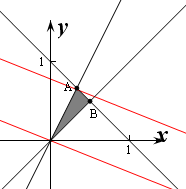
作出不等式组对应的平面区域如图:
由平移可知当直线y=-$\frac{1}{m}$x+$\frac{z}{m}$,
经过点A时,目标函数取得最大值,此时z=x+my=3,
由$\left\{\begin{array}{l}{y=2x}\\{x+y=1}\end{array}\right.$,解得A($\frac{1}{3}$,$\frac{2}{3}$),
同时,A也在直线x+my=3上,
代入得$\frac{1}{3}$+$\frac{2}{3}$m=3,解得m=4,
故选:C.
点评 本题主要考查线性规划的应用,根据目标函数的几何意义确定取得最大值的最优解是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
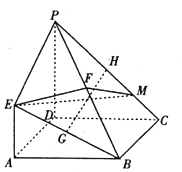 如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,G、H分别为BP、BE、PC的中点.
如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,G、H分别为BP、BE、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
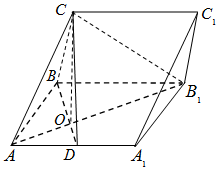 在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1.
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f′(x0)=0 | B. | f″(x0)>0 | ||
| C. | f′(x0)=0且f″(x0)>0 | D. | f′(x0)=0或f′(x0)不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一个命题的逆命题为真,则它的逆否命题一定为真 | |
| B. | 若“ac2>bc2”,则a>b | |
| C. | ?x0∈R,$sin{x_0}+cos{x_0}=\frac{3}{2}$ | |
| D. | “a2+b2=0,则a,b全为0”的逆否命题是“若a,b全不为0,则a2+b2≠0” |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com