
分析 根据平面向量的数量积的几何意义求向量的投影.
解答 解:因为向量$\overrightarrow a=({0,-2\sqrt{3}})$,$\overrightarrow b=({1,\sqrt{3}})$,
则向量$\overrightarrow a$在$\overrightarrow b$方向上的投影为$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}=\frac{-2\sqrt{3}×\sqrt{3}}{\sqrt{1+3}}=-3$;
故答案为:-3.
点评 本题考查了平面向量数量积的几何意义;熟记数量积公式是关键.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:选择题
| A. | 最小正周期为2π的偶函数 | B. | 最小正周期为2π的奇函数 | ||
| C. | 最小正周期为π的偶函数 | D. | 最小正周期为π的奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
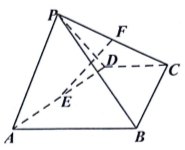 如图,在四棱锥P-ABCD中,△PAD为正三角形,四边形ABCD为直角梯形,CD∥AB,BC⊥AB,平面PAD⊥平面ABCD,点E、F分别为AD、CP的中点,AD=AB=2CD=2.
如图,在四棱锥P-ABCD中,△PAD为正三角形,四边形ABCD为直角梯形,CD∥AB,BC⊥AB,平面PAD⊥平面ABCD,点E、F分别为AD、CP的中点,AD=AB=2CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,3] | B. | [-$\frac{17}{5}$,3] | C. | [-$\frac{17}{5}$,1] | D. | [-$\frac{17}{5}$,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份202x(年) | 0 | 1 | 2 | 3 | 4 |
| 人口数 y(十万) | 5 | 7 | 8 | 11 | 19 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com