
| A. | 14 | B. | 13 | C. | 7 | D. | 6 |
分析 设等差数列{an}的首项为a1,把a6、a3、a7用a1 表示,由已知列式求得a1,写出Sn,利用二次函数求最值.
解答 解:设等差数列{an}的首项为a1,则a6=a1+10,a3=a1+4,a7=a1+12.
∵a6是a3和a7的等比中项,
∴${a}_{3}{a}_{7}={{a}_{6}}^{2}$,即$({a}_{1}+4)({a}_{1}+12)=({a}_{1}+10)^{2}$,
解得:a1=-13.
∴${S}_{n}=-13n+\frac{n(n-1)×2}{2}={n}^{2}-14n$.
由Sn<0,得n2-14n<0,解得0<n<14.
∴满足Sn<0的n的最大值为13.
故选:B.
点评 本题考查等差数列的性质,训练了利用二次函数求最值,是中档题.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:选择题
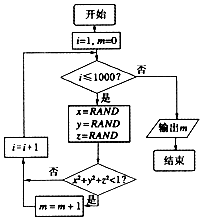 我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为527,则由此可估计π的近似值为( )
我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为527,则由此可估计π的近似值为( )| A. | 3.126 | B. | 3.132 | C. | 3.151 | D. | 3.162 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (-∞,1) | C. | (-1,+∞) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
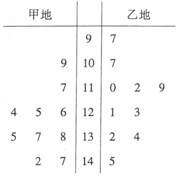 在一次期末模拟测试中,某市教研室在甲、乙两地各抽取了10名学生的数学成绩,得到茎叶图如图所示.
在一次期末模拟测试中,某市教研室在甲、乙两地各抽取了10名学生的数学成绩,得到茎叶图如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com