
分析 (1)由正弦定理,两角和的正弦函数公式化简已知可得2sinBcosA=sinB,结合sinB≠0,可求$cosA=\frac{1}{2}$;由A∈(0,π),可求A的值.
(2)由余弦定理,基本不等式可求bc≤12,进而利用三角形面积公式即可计算得解.
解答 (本小题满分12分)
解:(1)由(2b-c)cosA=acosC得:(2sinB-sinC)cosA=sinAcosC,…(2分)
即:2sinBcosA=sinAcosC+sinCcosA,
即2sinBcosA=sin(A+C)=sinB,…(4分)
∵sinB≠0,
∴$cosA=\frac{1}{2}$;
∵A∈(0,π),
∴$A=\frac{π}{3}$; …(6分)
(2)由余弦定理得:b2+c2-bc=12,
则:bc≤12,(当$b=c=2\sqrt{3}$时等号成立),…(8分)
∴${S_{△ABC}}=\frac{1}{2}bcsin\frac{π}{3}≤\frac{1}{2}×12×\frac{{\sqrt{3}}}{2}=3\sqrt{3}$,即△ABC面积的最大值为$3\sqrt{3}$;…(10分)
∴BC边上高的最大值为:$\frac{{2{{({S_{△ABC}})}_{max}}}}{a}=\frac{{2×3\sqrt{3}}}{{2\sqrt{3}}}=3$.…(12分)
点评 本题主要考查了正弦定理,两角和的正弦函数公式,余弦定理,基本不等式,三角形面积公式在解三角形中的综合应用,考查了计算能力和转化思想,属于基础题.


科目:高中数学 来源: 题型:选择题
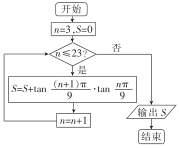
| A. | $-\frac{{2\sqrt{3}}}{{tan\frac{π}{9}}}-21$ | B. | $\frac{{tan\frac{25π}{9}-\sqrt{3}}}{{tan\frac{π}{9}}}-22$ | ||
| C. | $-\frac{{2\sqrt{3}}}{{tan\frac{π}{9}}}-22$ | D. | $\frac{{tan\frac{25π}{9}-\sqrt{3}}}{{tan\frac{π}{9}}}-21$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 14 | B. | 13 | C. | 7 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,3) | B. | [3,5] | C. | (-3,5] | D. | (-∞,-3)∪[-2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y=0 | B. | 2x+y-1=0 | C. | x-y=0 | D. | 2x-y-1=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com