
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,短轴长为2;
,短轴长为2;
(1)求椭圆的标准方程;
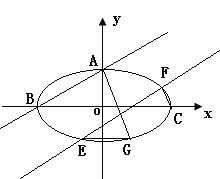
(2)设椭圆上顶点![]() ,左、右顶点分别为
,左、右顶点分别为![]() 、
、![]() .直线
.直线![]() 且交椭圆于
且交椭圆于![]() 、
、![]() 两点,点E 关于
两点,点E 关于![]() 轴的对称点为点
轴的对称点为点![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)由已知可得关于a,b,c的方程组,求解可得a,b,c的值,则椭圆方程可求;
(2)求出AB的斜率,得到直线l的斜率,设直线l的方程为y![]() x+m,E(x1,y1),F(x2,y2),则G(﹣x1,y1),联立直线方程与椭圆方程,然后利用根与系数的关系结合斜率公式证明CF∥AG.
x+m,E(x1,y1),F(x2,y2),则G(﹣x1,y1),联立直线方程与椭圆方程,然后利用根与系数的关系结合斜率公式证明CF∥AG.
(1)由题意可得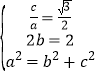 ,解得a2=4,b2=1,c2=3,
,解得a2=4,b2=1,c2=3,
∴椭圆的标准方程为![]() y2=1,
y2=1,
(2)由(1)可得A(0,1),B(﹣2,0),C(2,0),
∵直线l∥AB,∴kl=kAB![]() ,
,
不妨设直线l的方程为y![]() x+m,
x+m,
设![]() ,
,![]() ,则
,则![]() ,
,
![]()
![]() ,
,![]()
![]() ,
,
由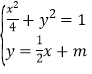 ,得:
,得:![]() ,得:
,得:![]() ,
,![]()
因为(![]() )
)![]()
![]()
![]()
=![]()
所以,![]()
![]()
![]() ,
,
即![]()
![]() ,
,
所以,![]() .
.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左右焦点分别为
的左右焦点分别为![]() 、
、![]() ,左右顶点分别是
,左右顶点分别是![]() 、
、![]() ,长轴长为
,长轴长为![]() ,
,![]() 是以原点为圆心,
是以原点为圆心,![]() 为半径的圆的任一条直径,四边形
为半径的圆的任一条直径,四边形![]() 的面积最大值为
的面积最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)不经过原点的直线![]() :
:![]() 与椭圆交于
与椭圆交于![]() 、
、![]() 两点,
两点,
①若直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,且
,且![]() ,求证:直线
,求证:直线![]() 过定点,并求出该定点的坐标;
过定点,并求出该定点的坐标;
②若直线![]() 的斜率是直线
的斜率是直线![]() 、
、![]() 斜率的等比中项,求
斜率的等比中项,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 上动点
上动点![]() 与定点
与定点![]() 的距离和它到定直线
的距离和它到定直线![]() 的距离的比是常数
的距离的比是常数![]() ,若过
,若过![]() 的动直线
的动直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点
两点
(1)说明曲线![]() 的形状,并写出其标准方程;
的形状,并写出其标准方程;
(2)是否存在与点![]() 不同的定点
不同的定点![]() ,使得
,使得![]() 恒成立?若存在,求出点
恒成立?若存在,求出点![]() 的坐标;若不存在,请说明理由
的坐标;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某地某月1日至15日的日平均温度变化的折线图,根据该折线图,下列结论正确的是( )
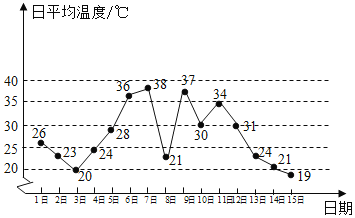
A. 这15天日平均温度的极差为![]()
B. 连续三天日平均温度的方差最大的是7日,8日,9日三天
C. 由折线图能预测16日温度要低于![]()
D. 由折线图能预测本月温度小于![]() 的天数少于温度大于
的天数少于温度大于![]() 的天数
的天数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 截直线
截直线![]() 所得的线段的长度为
所得的线段的长度为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 上的点,
上的点,![]() 是坐标原点,若
是坐标原点,若![]() ,判定四边形
,判定四边形![]() 的面积是否为定值?若为定值,求出定值;如果不是,请说明理由.
的面积是否为定值?若为定值,求出定值;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
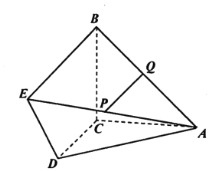
【题目】如图,DC⊥平面ABC,![]() ,
,![]() ,
,![]() ,P、Q分别为AE,AB的中点.
,P、Q分别为AE,AB的中点.
(1)证明:![]() 平面
平面![]() .
.
(2)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)求平面![]() 与平面
与平面![]() 所成锐二面角的大小。
所成锐二面角的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知抛物线的焦点F在y轴上,其准线与双曲线![]()
![]() 的下准线重合.
的下准线重合.

(1)求抛物线的标准方程;
(2)设A(![]() ,
,![]() )(
)(![]() >0)是抛物线上一点,且AF=
>0)是抛物线上一点,且AF=![]() ,B是抛物线的准线与y轴的交点.过点A作抛物线的切线l,过点B作l的平行线l′,直线l′与抛物线交于点M,N,求△AMN的面积.
,B是抛物线的准线与y轴的交点.过点A作抛物线的切线l,过点B作l的平行线l′,直线l′与抛物线交于点M,N,求△AMN的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com