
分析 由已知中f(a+b)=f(a)•f(b),可得:$\frac{{f}^{2}(\frac{a+1}{2})+f(a+1)}{f(a)}$=$\frac{2f(a+1)}{f(a)}$=2f(1)=4,进而得到答案.
解答 解:∵f(a+b)=f(a)•f(b),
∴$\frac{{f}^{2}(\frac{a+1}{2})+f(a+1)}{f(a)}$=$\frac{2f(a+1)}{f(a)}$=2f(1)=4,
∴$\frac{{f}^{2}(1)+f(2)}{f(1)}+\frac{{f}^{2}(2)+f(4)}{f(3)}+\frac{{f}^{2}(3)+f(6)}{f(5)}+…\frac{{f}^{2}(1008)+f(2016)}{f(2015)}$=4×$\frac{2015+1}{2}$=4032,
故答案为:4032
点评 本题考查的知识点是抽象函数及其应用,其中根据已知得到$\frac{{f}^{2}(\frac{a+1}{2})+f(a+1)}{f(a)}$=$\frac{2f(a+1)}{f(a)}$=2f(1)=4,是解答的关键.


科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(理)试卷(解析版) 题型:选择题
已知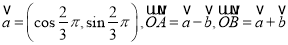 ,若
,若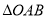 是以
是以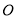 为直角顶点的等腰直角三角形,则
为直角顶点的等腰直角三角形,则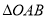 的面积等于( )
的面积等于( )
A.1 B. C.2 D.
C.2 D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2} | B. | {0,1,3} | C. | {0,2,3} | D. | {1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com