
分析 (Ⅰ)这种证明数列不是等差数列的问题实际上不好表述,我们可以选择反证法来证明,假设存在推出矛盾;
(Ⅱ)我们写出数列的第n+1项和第n项之间的关系,由等比数列的定义即可得到结论;
(Ⅲ)根据等比数列的求和公式写出数列的前n项和,把不等式写出来化简可得$\frac{\frac{1}{2}}{1-(-\frac{1}{2})^{n}}$≤m-$\frac{2}{9}$≤$\frac{1}{1-(-\frac{1}{2})^{n}}$,分别求得左右两边的最值即可,注意n的奇偶情况要分类讨论.
解答 解:(Ⅰ)证明:当m=1时,a1=1,an+1=λan+n,
假设对于任意的实数λ,{an}是等差数列,可设an=1+(n-1)d,
即有1+nd=λ[1+(n-1)d]+n,
即为1+nd=λ(1-d)+n(λd+1),
可得1=λ-λd,d=λd+1,
解得λ=d,d2-d+1=0,d∈∅,
故假设不成立,即有对于任意的实数λ,{an}一定不是等差数列;
(Ⅱ)当λ=-$\frac{1}{2}$,m≠$\frac{2}{9}$时,bn+1=an+1-$\frac{2}{3}$(n+1)+$\frac{4}{9}$
=-$\frac{1}{2}$an+n-$\frac{2}{3}$n-$\frac{2}{9}$=-$\frac{1}{2}$(an-$\frac{2n}{3}$+$\frac{4}{9}$)=-$\frac{1}{2}$bn,
由m≠$\frac{2}{9}$,可得b1=m-$\frac{2}{3}$+$\frac{4}{9}$≠0,
由等比数列的定义可得,{bn}为首项为m-$\frac{2}{9}$,公比为-$\frac{1}{2}$的等比数列;
(Ⅲ)假设存在实数m,使得对任意的正整数n,都有$\frac{1}{3}$≤Sn≤$\frac{2}{3}$.
由(Ⅱ)可得,Sn=$\frac{(m-\frac{2}{9})[1-(-\frac{1}{2})^{n}]}{1-(-\frac{1}{2})}$,
由$\frac{1}{3}$≤Sn≤$\frac{2}{3}$,可得$\frac{\frac{1}{2}}{1-(-\frac{1}{2})^{n}}$≤m-$\frac{2}{9}$≤$\frac{1}{1-(-\frac{1}{2})^{n}}$,
当n为奇数时,1-(-$\frac{1}{2}$)n>1,当n为偶数时,0<1-(-$\frac{1}{2}$)n<1,
即有$\frac{\frac{1}{2}}{1-(-\frac{1}{2})^{n}}$的最大值为$\frac{\frac{1}{2}}{1-\frac{1}{4}}$=$\frac{2}{3}$,则m-$\frac{2}{9}$≥$\frac{2}{3}$,
解得m≥$\frac{8}{9}$;
由n→+∞,可得(-$\frac{1}{2}$)n→0,故1-(-$\frac{1}{2}$)n→1,
即有m-$\frac{2}{9}$≤1,解得m≤$\frac{11}{9}$.
即有存在实数m,且m∈[$\frac{8}{9}$,$\frac{11}{9}$],
使得对任意的正整数n,都有$\frac{1}{3}$≤Sn≤$\frac{2}{3}$.
点评 本题考查等差数列和等比数列的定义和通项公式、求和公式的运用,考查反证法的运用和恒成立问题的解法,注意运用数列的最值的求法,属于中档题.


 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | (-∞,-1]∪[1,+∞) | C. | [-1,1] | D. | (-∞,0]∪[1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
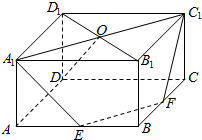 如图.在直四棱柱ABCD-A1B1C1D1中,E,F分別AB,BC的中点,A1C1与B1D1交于点O.
如图.在直四棱柱ABCD-A1B1C1D1中,E,F分別AB,BC的中点,A1C1与B1D1交于点O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com