
| A. | $[{\frac{{\sqrt{3}}}{2},1})$ | B. | $[{\frac{1}{2},1})$ | C. | $({0,\frac{{\sqrt{3}}}{2}}]$ | D. | $({0,\frac{1}{2}}]$ |
分析 先根据椭圆定义得到|PF1|=a+ex1,|PF2|=a-ex1,再利用余弦定理得到余弦定理得cos$\frac{2π}{3}$=-$\frac{1}{2}$=$\frac{(a+{ex}_{1})^{2}+(a-e{x}_{1})^{2}-4{c}^{2}}{2(a+e{x}_{1})(a-e{x}_{1})}$,求出 x12=$\frac{4{c}^{2}-3{a}^{2}}{{e}^{2}}$,利用椭圆的范围列出不等式求出离心率的范围.
解答 解:设,P(x1,y1),F1(-c,0),F2(c,0),c>0,
则|PF1|=a+ex1,|PF2|=a-ex1.
在△PF1F2中,由余弦定理得 cos$\frac{2π}{3}$=-$\frac{1}{2}$=$\frac{(a+{ex}_{1})^{2}+(a-e{x}_{1})^{2}-4{c}^{2}}{2(a+e{x}_{1})(a-e{x}_{1})}$,
解得 x12=$\frac{4{c}^{2}-3{a}^{2}}{{e}^{2}}$,.
∵x12∈(0,a2],
∴0≤$\frac{4{c}^{2}-3{a}^{2}}{{e}^{2}}$<a2,
即4c2-3a2≥0.且e2<1
∴e=$\frac{c}{a}$≥$\frac{\sqrt{3}}{2}$.
故椭圆离心率的取范围是 e∈[$\frac{\sqrt{3}}{2}$,1).
故选:A.
点评 本题主要考查了椭圆的应用.当P点在短轴的端点时∠F1PF2值最大,这个结论可以记住它.在做选择题和填空题的时候直接拿来解决这一类的问题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a⊥α,b?α,则a⊥b | B. | 若a⊥α,a∥b,则b⊥α | ||
| C. | 若a⊥b,b⊥α,则a∥α或a?α | D. | 若a∥α,b?α,则a∥b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
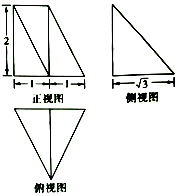 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | 3$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{4}{3}$$\sqrt{3}$ | D. | $\frac{5}{3}$$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com