
分析 (1)分直线斜率存在与否,两种情况解答;
(2)把直线y=ax+1代入圆C的方程d得到关于x的一元二次方程,利用交点个数与判别式的关系得到a的范围,设符合条件的实数a存在,利用直线垂直的斜率关系得到a值判断.
解答 解:(1)设直线l的斜率为k(k存在),
则方程为y-0=k(x-2).即kx-y-2k=0
又圆C的圆心为(3,-2),半径r=3,
由 $\frac{{|{3k+2-2k}|}}{{\sqrt{{k^2}+1}}}=1$,解得$k=-\frac{3}{4}$.
所以直线方程为$y=-\frac{3}{4}(x-2)$,即 3x+4y-6=0.
当l的斜率不存在时,l的方程为x=2,经验证x=2也满足条件.
(2)把直线y=ax+1.代入圆C的方程,
消去y,整理得(a2+1)x2+6(a-1)x+9=0.
由于直线ax-y-1=0交圆C于A,B两点,
故△=36(a-1)2-36(a2+1)>0,
即-2a>0,解得a<0.则实数a的取值范围是(-∞,0).
设符合条件的实数a存在,
由于l2垂直平分弦AB,故圆心C(3,-2)必在l2上.
所以l2的斜率kPC=-2,而${k_{AB}}=a=-\frac{1}{{{k_{PC}}}}$,所以$a=\frac{1}{2}$.由于$\frac{1}{2}∉(-∞,0)$,
故不存在实数a,使得过点P(2,0)的直线l2垂直平分弦AB.
点评 本题考查了直线方程的求法以及直线与圆的位置关系的判断;属于中档题.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
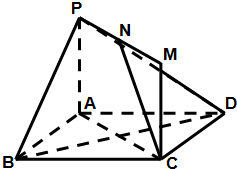 如图,矩形ACMP和菱形ABCD所在的平面互相垂直,点N为PM的中点,
如图,矩形ACMP和菱形ABCD所在的平面互相垂直,点N为PM的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 正四面体ABCD的棱长为2,棱AD与平面α所成的角θ∈[$\frac{π}{3}$,$\frac{π}{2}$],且顶点A在平面α内,B,C,D均在平面α外,则棱BC的中点E到平面α的距离的取值范围是( )
正四面体ABCD的棱长为2,棱AD与平面α所成的角θ∈[$\frac{π}{3}$,$\frac{π}{2}$],且顶点A在平面α内,B,C,D均在平面α外,则棱BC的中点E到平面α的距离的取值范围是( )| A. | [$\frac{\sqrt{3}}{2}$,1] | B. | [$\frac{\sqrt{3}-\sqrt{2}}{2}$,1] | C. | [$\frac{\sqrt{3}-\sqrt{2}}{2}$,$\frac{\sqrt{3}+\sqrt{2}}{2}$] | D. | [$\frac{\sqrt{3}-\sqrt{2}}{2}$,$\sqrt{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com