练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某商品促销活动设计了一个摸奖游戏：在一个口袋中装有4个红球和6个白球，这些球除颜色外完全相同，顾客一次从中摸出3个球，若3个都是白球则无奖励，若有1个红球则奖励10元购物券，若有2个红球则奖励20元购物券，若3个都是红球则奖励30元购物券.

    （Ⅰ）求中奖的概率；

    （Ⅱ）求顾客摸奖一次获得购物券奖励的平均值.

    【答案】（Ⅰ）（Ⅱ）顾客摸奖一次获得购物券奖励的平均值为12元

    【解析】

    （Ⅰ）利用对立事件的概率公式求中奖的概率. （Ⅱ）设顾客摸奖一次获得购物券奖励元，则，再求出对应的概率，再求出顾客摸奖一次获得购物券奖励的平均值.

    （Ⅰ）中奖的概率

    （Ⅱ）顾客摸奖一次获得购物券奖励元，则

    所以的分布列为

    0

    10

    20

    30

    答：顾客摸奖一次获得购物券奖励的平均值为12元.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某地区不同身高的未成年男性的体重平均值如下表.

    身高/

    60

    70

    80

    90

    100

    110

    120

    130

    140

    150

    160

    170

    体重/

    6.13

    7.90

    9.99

    12.15

    15.02

    17.50

    20.92

    26.86

    31.11

    38.85

    47.25

    55.05

    （1）根据表格提供的数据，能否建立恰当的函数模型，使它能比较近似地反映这个地区未成年男性体重与身高的函数关系？试写出这个函数模型的关系式.

    （2）若体重超过相同身高男性体重平均值的1.2倍为偏胖，低于0.8倍为偏瘦，那么这个地区一名身高为，体重为的在校男生的体重是否正常？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】以下命题，①若实数，则．

    ②归纳推理是由特殊到一般的推理，而类比推理是由特殊到特殊的推理；

    ③在回归直线方程中，当变量每增加一个单位时，变量一定增加0．2单位．

    ④“若，则复数”类比推出“若，则”；

    正确的个数是（ ）

    A. 1B. 2C. 3D. 4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校为调查高三年级学生的身高情况，按随机抽样的方法抽取80名学生，得到男生身高情况的频率分布直方图（图1）和女生身高情况的频率分布直方图（图2）.已知图1中身高在170～175cm的男生人数有16人

    .

    (1)根据频率分布直方图，完成下列的列联表，并判断能有多大（百分比）的把握认为“身高与性别有关”？

    总计

    男生身高

    女生身高

    总计

    (2)在上述80名学生中，从身高在170-175cm之间的学生按男、女性别分层抽样的方法，抽出5人，从这5人中选派3人当旗手，求3人中恰好有一名女生的概率.

    0.025

    0.610

    0.005

    0.001

    5.024

    4.635

    7.879

    10.828

    参考公式及参考数据如下：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆离心率为，四个顶点构成的四边形的面积是4.

    (Ⅰ)求椭圆的方程；

    (Ⅱ)若直线与椭圆交于均在第一象限，与轴、轴分别交于、两点，设直线的斜率为,直线的斜率分别为，且(其中为坐标原点).证明: 直线的斜率为定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】袋子中有5个大小质地完全相同的球，其中2个红球、3个黄球，从中不放回地依次随机摸出2个球，求下列事件的概率：

    （1）A=“第一次摸到红球”；

    （2）B=“第二次摸到红球”；

    （3）AB=“两次都摸到红球”.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在直角坐标系中，以坐标原点为极点，以轴正半轴为极轴，建立极坐标系，圆的方程为，直线的极坐标方程为.

    (I )写出的极坐标方程和的平面直角坐标方程;

    (Ⅱ) 若直线的极坐标方程为,设与的交点为与的交点为求的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ．

    （1）当时，若函数恰有一个零点，求实数的取值范围；

    （2）当， 时，对任意，有成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】[选修4－4：坐标系与参数方程]

    在平面直角坐标系中，直线的参数方程为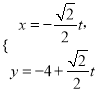（其中t为参数），现以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为．

    （1）写出直线l普通方程和曲线C的直角坐标方程；

    （2）过点且与直线平行的直线交于， 两点，求.

    查看答案和解析>>

    同步练习册答案