
【题目】已知椭圆![]() 离心率为
离心率为![]() ,四个顶点构成的四边形的面积是4.
,四个顶点构成的四边形的面积是4.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 均在第一象限,
均在第一象限,![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,设直线
两点,设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率分别为
的斜率分别为![]() ,且
,且![]() (其中
(其中![]() 为坐标原点).证明: 直线
为坐标原点).证明: 直线![]() 的斜率为定值.
的斜率为定值.
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .设
.设![]() ,
,![]() 分别为
分别为![]() ,
,![]() 中点.
中点.
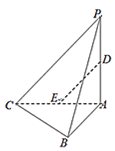
(1)求证:![]()
![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)试问在线段![]() 上是否存在点
上是否存在点![]() ,使得过三点
,使得过三点![]() ,
,![]() ,
,![]() 的平面内的任一条直线都与平面
的平面内的任一条直线都与平面![]() 平行?若存在,指出点
平行?若存在,指出点![]() 的位置并证明;若不存在,请说明理由.
的位置并证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农产品从5月1日起开始上市,通过市场调查,得到该农产品种植成本Q(单位:元/![]() )与上市时间t(单位:天)的数据如下表:
)与上市时间t(单位:天)的数据如下表:
t | 50 | 110 | 250 |
Q | 150 | 108 | 150 |
(1)根据上表数据,从下列函数中选取一个函数描述该农产品种植成本Q与上市时间t的变化关系,并求出函数关系式:![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)利用你选取的函数,求该农产品种植成本最低时的上市时间及最低种植成本.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有4种不同颜色要对如图所示的四个部分进行着色,要求有公共边界的两部分不能用同一种颜色,则不同的着色方法共有( )

A. 144种 B. 72种 C. 64种 D. 84种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品促销活动设计了一个摸奖游戏:在一个口袋中装有4个红球和6个白球,这些球除颜色外完全相同,顾客一次从中摸出3个球,若3个都是白球则无奖励,若有1个红球则奖励10元购物券,若有2个红球则奖励20元购物券,若3个都是红球则奖励30元购物券.
(Ⅰ)求中奖的概率;
(Ⅱ)求顾客摸奖一次获得购物券奖励的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ;②
;②![]() 这两个条件中任选-一个,补充在下面问题中,然后解答补充完整的题.
这两个条件中任选-一个,补充在下面问题中,然后解答补充完整的题.

在![]() 中,角
中,角![]() 的对边分别为
的对边分别为![]() ,已知 ,
,已知 ,![]() .
.
(1)求![]() ;
;
(2)如图,![]() 为边
为边![]() 上一点,
上一点,![]() ,求
,求![]() 的面积
的面积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
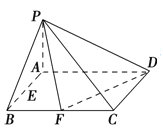
(1)证明:PF⊥FD;
(2)判断并说明PA上是否存在点G,使得EG∥平面PFD;
(3)若PB与平面ABCD所成的角为45°,求二面角A-PD-F的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com