
分析 构造函数f(x)=-4x2+4ax-4a-a2+5.x∈[0,1].
分类讨论(1)当△≤0时,即a$≤-\frac{5}{4}$,f(x)≤0恒成立,
(2)当△>0时,即a$>-\frac{5}{4}$,利用对称轴的位置得出不等式组只需$\left\{\begin{array}{l}{\frac{a}{2}≥1}\\{f(1)=-4+4a-4a-{a}^{2}+5≤0}\end{array}\right.$或$\left\{\begin{array}{l}{\frac{a}{2}≤0}\\{f(0)=-4a-{a}^{2}+5≤0}\end{array}\right.$求解即可.
解答 解:设函数f(x)=-4x2+4ax-4a-a2+5.x∈[0,1].
对称轴x=$\frac{a}{2}$,△=16a2-4×(-4)×(-4a-a2+5)=64a+80,
(1)当△≤0时,即a$≤-\frac{5}{4}$,f(x)≤0恒成立,
即0≤x≤1时,不等式-4x2+4ax-4a-a2≤-5恒成立,
(2)当△>0时,即a$>-\frac{5}{4}$,
要使0≤x≤1时,不等式-4x2+4ax-4a-a2≤-5恒成立,
只需$\left\{\begin{array}{l}{\frac{a}{2}≥1}\\{f(1)=-4+4a-4a-{a}^{2}+5≤0}\end{array}\right.$或$\left\{\begin{array}{l}{\frac{a}{2}≤0}\\{f(0)=-4a-{a}^{2}+5≤0}\end{array}\right.$
求解得出$\left\{\begin{array}{l}{a≥2}\\{a≥1或a≤-1}\end{array}\right.$或$\left\{\begin{array}{l}{a≤0}\\{a≥1或a≤-5}\end{array}\right.$,
即可得出a≥2,使0≤x≤1时,不等式-4x2+4ax-4a-a2≤-5恒成立,
有(1)(2)得出a≥2或a$≤-\frac{5}{4}$.
故答案为:a≥2或a$≤-\frac{5}{4}$.
点评 本题综合考察了二次函数性质的运用求解函数最值与不等式恒成立问题的运用,关键分类讨论得出不等式组即可.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:填空题
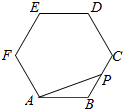 如图所示:点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=4,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间[-8,24].
如图所示:点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=4,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间[-8,24].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{7}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com