
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
分析 根据向量的定义,零向量和任何向量平行,数量积的计算公式即可判断每个命题的真假,从而找出正确选项.
解答 解:(1)$|\overrightarrow{a}|=|\overrightarrow{b}|$是说明长度关系,不能判断方向关系;
∴得不到$\overrightarrow{a}=\overrightarrow{b}$,或$\overrightarrow{a}=-\overrightarrow{b}$;
∴该命题错误;
(2)$\overrightarrow{b}=\overrightarrow{0}$,$\overrightarrow{a},\overrightarrow{c}$不共线时,仍满足$\overrightarrow{a}∥\overrightarrow{b}$,$\overrightarrow{b}∥\overrightarrow{c}$;
∴得不出$\overrightarrow{a}∥\overrightarrow{c}$;
∴该命题错误;
(3)$\overrightarrow{a}•\overrightarrow{c}=\overrightarrow{b}•\overrightarrow{c}$;
∴$(\overrightarrow{a}-\overrightarrow{b})•\overrightarrow{c}=0$;
∴$(\overrightarrow{a}-\overrightarrow{b})⊥\overrightarrow{c}$,不能说明$\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{0}$;
∴得不出$\overrightarrow{a}=\overrightarrow{b}$;
∴该命题错误.
故选:D.
点评 考查向量的定义,零向量的概念,平行向量的定义,以及数量积的计算公式.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
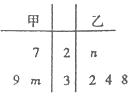 已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同.
已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{e}$ | C. | $\frac{1}{e^2}$ | D. | $\frac{1}{{\sqrt{e}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com