
分析 由题意知将A、B分别分解为互斥事件,利用互斥事件来表示要比较的两个事件的概率,根据等可能事件的概率写出P(A1)与P(A2),P(B1)与P(B2),利用互斥事件的概率表示出A与B的概率,根据基本不等式进行比较得到结果.
解答 解:基本事件总数为(m+n)2,“两球同色”可分为“两球皆白”或“两球皆黑”,
则$P(A)=\frac{mn}{{{{({m+n})}^2}}}+\frac{mn}{{{{({m+n})}^2}}}=\frac{2mn}{{{{({m+n})}^2}}}$,
“两球异色”可分为“一白一黑”或“一黑一白”,
则$P(B)=\frac{m^2}{{{{({m+n})}^2}}}+\frac{n^2}{{{{({m+n})}^2}}}=\frac{{{m^2}+{n^2}}}{{{{({m+n})}^2}}}$,
∵$P(B)-P(A)=\frac{{{{({m-n})}^2}}}{{{{({m+n})}^2}}}≥0$,
∴P(A)≤P(B),当且仅当“m=n”时取等号.
点评 由题意知本题也可以这样解:显然B=$\overline{A}$,所以按解法一解出P(A)后,可得P(B)=1-P(A)=$\frac{{m}^{2}{+n}^{2}}{{(m+n)}^{2}}$,比较P(A)、P(B)即可.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{2017}{2}$ | B. | $\frac{2}{2017}$ | C. | $\frac{1}{2016}$ | D. | $\frac{1}{1008}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
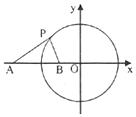 已知圆C:x2+y2=9,点A(-5,0),直线l:x-2y=0.
已知圆C:x2+y2=9,点A(-5,0),直线l:x-2y=0.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(b)<f(a)<f(c) | B. | f(c)<f(b)<f(a) | C. | f(c)<f(a)<f(b) | D. | f(b)<f(c)<f(a) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{1}{4}$) | B. | (0,+∞) | C. | (-∞,-$\frac{1}{4}$)∪(0,+∞) | D. | (-$\frac{1}{4}$,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com