
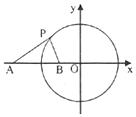
 已知圆C:x2+y2=9,点A(-5,0),直线l:x-2y=0.
已知圆C:x2+y2=9,点A(-5,0),直线l:x-2y=0.分析 (1)根据所求直线与直线l垂直,设所求直线方程为y=-2x+b,即2x+y-b=0,利用直线与圆相切,距离d=r可得b的值,可得直线方程.
(2)设出P点,利用两点之间的距离公式,求解BP和PA,化简可得结论.
解答 解:(1)由题意,所求直线与直线l垂直,
设所求直线方程为y=-2x+b,即2x+y-b=0,
∵直线与圆相切,∴$\frac{|-b|}{{\sqrt{{2^2}+{1^2}}}}=3$,得$b=±3\sqrt{5}$,
∴所求直线方程为$y=-2x±3\sqrt{5}$.
(2)圆C上任一点为P,设P(x,y),则y2=9-x2,
∴$\frac{{P{B^2}}}{{P{A^2}}}=\frac{{{{(x+\frac{9}{5})}^2}+{y^2}}}{{{{(x+5)}^2}+{y^2}}}=\frac{{{x^2}+\frac{18}{5}x+\frac{81}{25}+9-{x^2}}}{{{x^2}+10x+25+9-{x^2}}}=\frac{{\frac{18}{25}(5x+17)}}{2(5x+17)}=\frac{9}{25}$,
从而$\frac{PB}{PA}=\frac{3}{5}$为常数.
点评 本题主要考查直线和圆的位置关系的运用,根据直线和圆相切距离d=r是解决本题的关键.同时考查了两点之间的距离公式的运用和计算能力.属于中档题.


 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形BCDE是直角梯形,CD∥BE,CD丄BC,CD=$\frac{1}{2}$BE=2,平面BCDE丄平面ABC,又已知△ABC为等腰直角三角形,AB=AC=4,M是BC的中点.
如图,四边形BCDE是直角梯形,CD∥BE,CD丄BC,CD=$\frac{1}{2}$BE=2,平面BCDE丄平面ABC,又已知△ABC为等腰直角三角形,AB=AC=4,M是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e2+3 | B. | e2+4 | C. | e+1 | D. | e+2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com