
分析 (1)选择②式由sin215°+cos215°-sin15°cos15°=1-$\frac{1}{2}sin30°$=$\frac{3}{4}$,可得这个常数的值.
(2)推广,得到三角恒等式sin2α+cos2(30°-α)-sinαcos(30°-α)=$\frac{3}{4}$,直接利用两角差的余弦公式代入等式的左边,化简可得结果.
解答 解:(1)选择②式,计算如下:sin215°+cos215°-sin15°cos15°=1-$\frac{1}{2}sin30°$=$\frac{3}{4}$;------(4分),
(2)三角恒等式为sin2α+cos2(30°-α)-sinαcos(30°-α)=$\frac{3}{4}$,---(6分)
证明如下:sin2α+cos2(30°-α)-sinαcos(30°-α)=sin2α+(cos30°cosα+sin30°sinα)2-sinα(cos30°cosα+sin30°sinα)---(7分),
=sin2α+($\frac{\sqrt{3}}{2}$cosα+$\frac{1}{2}$sinα)2-sinα($\frac{\sqrt{3}}{2}$cosα+$\frac{1}{2}$sinα)=$\frac{3}{4}$sin2α+$\frac{3}{4}$cos2α=$\frac{3}{4}$---(12分),
点评 本题主要考查两角差的余弦公式,二倍角公式的应用,考查归纳推理以及计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (x+1)2+y2=2 | B. | x2+(y+2)2=2 | ||
| C. | (x+3)2+y2=2 | D. | (x+1)2+y2=2或(x+3)2+y2=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
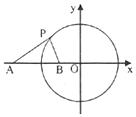 已知圆C:x2+y2=9,点A(-5,0),直线l:x-2y=0.
已知圆C:x2+y2=9,点A(-5,0),直线l:x-2y=0.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{6}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $-\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ③④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com