练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．已知正四棱锥的底面边长是2cm，侧棱长是$\sqrt{3}$cm，则该正四棱锥的体积为$\frac{4}{3}c{m}^{3}$．

    分析 正四棱锥P-ABCD中，AB=2，PA=$\sqrt{3}$，设正四棱锥的高为PO，连结AO，求出PO，由此能求出该正四棱锥的体积．

    解答 解：如图，正四棱锥P-ABCD中，AB=2cm，PA=$\sqrt{3}$cm，
    设正四棱锥的高为PO，连结AO，
    则AO=$\frac{1}{2}$AC=$\sqrt{2}$（cm）．
    在直角三角形POA中，PO=$\sqrt{P{A}^{2}-A{O}^{2}}$=$\sqrt{3-2}$=1（cm）．
    所以VP-ABCD=$\frac{1}{3}$•SABCD•PO=$\frac{1}{3}$×4×1=$\frac{4}{3}$（cm3）．
    故答案为：$\frac{4}{3}$cm3

    点评 本题考查正四棱锥的体积的求法，考查数据处理能力、运算求解能力以及应用意识，考查数形结合思想等，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    15．在10件产品中，有8种合格品，2件次品，从这10件产品中任意抽出3件，抽出的3件中至少有1件是次品的抽法种数为（　　）
    A．64B．72C．384D．432

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．若函数f（x）=$\frac{1}{3}{x^3}+a{x^2}$+bx+c有极值点x1，x2（x1＜x2），且f（x1）=x1，则关于x的方程[f（x）]2+2af（x）+b=0的不同实数根的个数为（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．下列不等式中，正确的是（　　）
    A．$tan\frac{13π}{4}＞tan\frac{13π}{3}$B．$sin\frac{π}{5}＞cos\frac{π}{5}$C．$cos\frac{3π}{5}＜cos（-\frac{2π}{5}）$D．cos 55°＞tan 35°

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知a＞0，求证：$\sqrt{{a^2}+\frac{1}{a^2}}$-$\sqrt{2}$≥a+$\frac{1}{a}-2$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知△ABC的三个内角A，B，C满足2017cos2C-cos2A=2016-2sin2B，则$\frac{tanC•（tanA+tanB）}{tanA•tanB}$=（　　）
    A．$\frac{2017}{2}$B．$\frac{2}{2017}$C．$\frac{1}{2016}$D．$\frac{1}{1008}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．在平行六面体ABCD-A1B1C1D1中，AB=2，AD=3，AA1=1，∠BAD=90°，∠BAA1=∠DAA1=60°，则对角线AC1的长为$\sqrt{19}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．圆心在x轴上，半径长为 $\sqrt{2}$，且过点（-2，1）的圆的方程为（　　）
    A．（x+1）2+y2=2B．x2+（y+2）2=2
    C．（x+3）2+y2=2D．（x+1）2+y2=2或（x+3）2+y2=2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

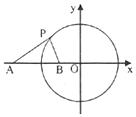    15．已知圆C：x2+y2=9，点A（-5，0），直线l：x-2y=0．
    （1）求与圆C相切，且与直线l垂直的直线方程；
    （2）设定点$B（-\frac{9}{5}，0）$，问：对于圆C上任一点P，$\frac{PB}{PA}$是否为一常数？若是，求出这个常数值；若不是，请说明理由．

    查看答案和解析>>

    同步练习册答案