Question

16．若函数f（x）=$\frac{1}{3}{x^3}+a{x^2}$+bx+c有极值点x₁，x₂（x₁＜x₂），且f（x₁）=x₁，则关于x的方程[f（x）]²+2af（x）+b=0的不同实数根的个数为（　　）

• A． 1
• B． 2
• C． 3
• D． 4

Answer 1

分析 函数f（x）=$\frac{1}{3}{x^3}+a{x^2}$+bx+c有两个极值点x₁，x₂，f′（x）=x²+2ax+b=0有两个不相等的实数根，△=4a²-4b＞0．而方程（f（x））²+2af（x）+b=0的△₁=△＞0，可知此方程有两解且f（x）=x₁或x₂．再分别讨论利用平移变换即可解出方程f（x）=x₁或f（x）=x₂解得个数．

解答 解：函数f（x）=$\frac{1}{3}{x^3}+a{x^2}$+bx+c有两个极值点x₁，x₂，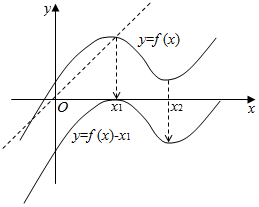
∴f′（x）=x²+2ax+b=0有两个不相等的实数根，
∴△=4a²-4b＞0．
而方程（f（x））²+2af（x）+b=0的△₁=△＞0，
∴此方程有两解且f（x）=x₁或x₂，
不妨取0＜x₁＜x₂，f（x₁）＞0．
①把y=f（x）向下平移x₁个单位即可得到y=f（x）-x₁的图象，
∵f（x₁）=x₁，可知方程f（x）=x₁有两解．
②把y=f（x）向下平移x₂个单位即可得到y=f（x）-x₂的图象，∵f（x₁）=x₁，∴f（x₁）-x₂＜0，可知方程f（x）=x₂只有一解．
综上①②可知：方程f（x）=x₁或f（x）=x₂．只有3个实数解．即关于x的方程3（f（x））²+af（x）+b=0的只有3不同实根．
故选：C．

点评 本题考查了利用导数研究函数的单调性极值、方程的解转化为函数图象的交点，考查了推理能力与计算能力，属于难题．