
【题目】记函数![]() 的定义域为D. 如果存在实数
的定义域为D. 如果存在实数![]() 、
、![]() 使得
使得![]() 对任意满
对任意满
足![]() 且
且![]() 的x恒成立,则称
的x恒成立,则称![]() 为
为![]() 函数.
函数.
(1)设函数![]() ,试判断
,试判断![]() 是否为
是否为![]() 函数,并说明理由;
函数,并说明理由;
(2)设函数![]() ,其中常数
,其中常数![]() ,证明:
,证明: ![]() 是
是![]() 函数;
函数;
(3)若![]() 是定义在
是定义在![]() 上的
上的![]() 函数,且函数
函数,且函数![]() 的图象关于直线
的图象关于直线![]() (m为常数)对称,试判断
(m为常数)对称,试判断![]() 是否为周期函数?并证明你的结论.
是否为周期函数?并证明你的结论.
【答案】(1) 是![]() 函数(2)见解析(3) 函数
函数(2)见解析(3) 函数![]() 为周期函数
为周期函数
【解析】试题分析: ![]() 求出
求出![]() 的定义域,
的定义域, ![]() 对任意
对任意![]() 恒成立转化成
恒成立转化成![]() 对任意
对任意![]() 恒成立,解出
恒成立,解出![]() ,使得
,使得
![]() 为
为![]() 函数
函数![]() 只需证明存在实数
只需证明存在实数![]() ,
, ![]() 使得当
使得当![]() 且
且![]() 时,
时, ![]() 恒成立,化简求得
恒成立,化简求得![]() ,
, ![]() ,满足条件
,满足条件![]() 图象关于直线
图象关于直线![]() 对称,结合
对称,结合![]() ,整体换元得
,整体换元得![]() ,从而证明结论
,从而证明结论
解析:(1)![]() 是
是![]() 函数
函数
理由如下: ![]() 的定义域为
的定义域为![]() ,
,
只需证明存在实数![]() ,
, ![]() 使得
使得![]() 对任意
对任意![]() 恒成立.
恒成立.
由![]() ,得
,得![]() ,即
,即![]() .
.
所以![]() 对任意
对任意![]() 恒成立. 即
恒成立. 即![]()
从而存在![]() ,使
,使![]() 对任意
对任意![]() 恒成立.
恒成立.
所以![]() 是
是![]() 函数.
函数.
(2)记![]() 的定义域为
的定义域为![]() ,只需证明存在实数
,只需证明存在实数![]() ,
, ![]() 使得当
使得当![]() 且
且![]() 时,
时,
![]() 恒成立,即
恒成立,即![]() 恒成立.
恒成立.
所以![]() ,
,
化简得, ![]() .
.
所以![]() ,
, ![]() . 因为
. 因为![]() ,可得
,可得![]() ,
, ![]() ,
,
即存在实数![]() ,
, ![]() 满足条件,从而
满足条件,从而![]() 是
是![]() 函数.
函数.
(3)函数![]() 的图象关于直线
的图象关于直线![]() (
(![]() 为常数)对称,
为常数)对称,
所以![]() (1),
(1),
又因为![]() (2),
(2),
所以当![]() 时,
时, ![]()
由(1) ![]()
由(2) ![]() (3)
(3)
所以![]()
(取![]() 由(3)得)
由(3)得)
再利用(3)式, ![]() .
.
所以![]() 为周期函数,其一个周期为
为周期函数,其一个周期为![]() .
.
当![]() 时,即
时,即![]() ,又
,又![]() ,
,
所以![]() 为常数. 所以函数
为常数. 所以函数![]() 为常数函数,
为常数函数,
![]() ,
, ![]() 是一个周期函数.
是一个周期函数.
综上,函数![]() 为周期函数
为周期函数


科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,过
,过![]() 的直线交椭圆于
的直线交椭圆于![]() ,
,![]() 两点,若椭圆
两点,若椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 的周长为16.
的周长为16.
(1)求椭圆![]() 的方程;
的方程;
(2)设不经过椭圆的中心而平行于弦![]() 的直线交椭圆
的直线交椭圆![]() 于点
于点![]() ,
,![]() ,设弦
,设弦![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() .证明:
.证明:![]() ,
,![]() ,
,![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了一二线城市的大街小巷.为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了200人进行抽样分析,得到下表(单位:人):
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了200人进行抽样分析,得到下表(单位:人):
经常使用 | 偶尔或不用 | 合计 | |
30岁及以下 | 70 | 30 | 100 |
30岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用共享单车情况与年龄有关?
市使用共享单车情况与年龄有关?
(2)现从所有抽取的30岁以上的网民中利用分层抽样抽取5人,
![]() 求这5人中经常使用、偶尔或不用共享单车的人数;
求这5人中经常使用、偶尔或不用共享单车的人数;
![]() 从这5人中,在随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用共享单车的概率.
从这5人中,在随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用共享单车的概率.
参考公式: 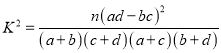 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各题中,![]() 是
是![]() 的什么条件?
的什么条件?
(1)![]() 为自然数,
为自然数,![]() 为整数;
为整数;
(2)![]() ;
;
(3)![]() ;
;
(4)![]() :四边形的一组对边相等,
:四边形的一组对边相等,![]() :四边形为平行四边形;
:四边形为平行四边形;
(5)![]() :四边形的对角线互相垂直,
:四边形的对角线互相垂直,![]() :四边形为菱形.
:四边形为菱形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中有如下问题:今有蒲生一日,长三尺,莞生一日,长1尺.蒲生日自半,莞生日自倍.问几何日而长等?意思是:今有蒲第一天长高3尺,莞第一天长高1尺,以后蒲每天长高前一天的一半,莞每天长高前一天的2倍.若蒲、莞长度相等,则所需时间为()
(结果精确到0.1.参考数据:lg2=0.3010,lg3=0.4771.)
A.2.6天B.2.2天C.2.4天D.2.8天
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂拟建一座平面图为矩形,面积为![]() ,高度一定的三段污水处理池(如图),由于受地形限制,其长、宽都不超过
,高度一定的三段污水处理池(如图),由于受地形限制,其长、宽都不超过![]() ,如果池的外壁的建造费单价为
,如果池的外壁的建造费单价为![]() 元
元![]() ,池中两道隔壁墙(与宽边平行)的建造费单价为
,池中两道隔壁墙(与宽边平行)的建造费单价为![]() 元
元![]() ,池底的建造费单价为
,池底的建造费单价为![]() 元
元![]() .设水池的长为
.设水池的长为![]() ,总造价为
,总造价为![]() .
.

(1)求![]() 的表达式;
的表达式;
(2)水池的长与宽各是多少时,总造价最低,并求出这个最低造价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com