
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,若对任意
时,若对任意![]() 均有
均有![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(2)设直线![]() 与曲线
与曲线![]() 和曲线
和曲线![]() 相切,切点分别为
相切,切点分别为![]() ,
,![]() ,其中
,其中![]() .
.
①求证:![]() ;
;
②当![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥PABCD中,PA⊥底面ABCD,AD∥BC,AB=AC=AD=3,PA=BC=4.
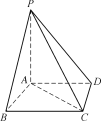
(1)求异面直线PB与CD所成角的余弦值;
(2)求平面PAD与平面PBC所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的有( )
①用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越小,说明模型的拟合效果越好;
越小,说明模型的拟合效果越好;
②若一组数据8,12,x,11,9的平均数是10,则其方差是2;
③回归直线一定过样本点的中心(![]() );
);
④若相关系数![]() ,则两个变量之间线性关系性强.
,则两个变量之间线性关系性强.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某游乐园的一个摩天轮半径为10米,轮子的底部在地面上2米处,如果此摩天轮每20分钟转一圈,当摩天轮上某人经过![]() 处时开始计时(按逆时针方向转),
处时开始计时(按逆时针方向转),![]() (其中
(其中![]() 平行于地面).
平行于地面).
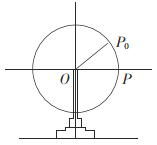
(1)求开始转动5分钟时此人相对于地面的高度.
(2)开始转动![]() 分钟时,摩天轮上此人经过点
分钟时,摩天轮上此人经过点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() ,
, ![]() ,
, ![]() 分别为椭圆的右顶点、上顶点和右焦点,且
分别为椭圆的右顶点、上顶点和右焦点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() :
: ![]() 被圆
被圆![]() :
: ![]() 所截得的弦长为
所截得的弦长为![]() ,若直线
,若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com