考点:数列与不等式的综合,等比数列的性质,数列递推式
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件推导出{a
n}是首项为a,公比为t的等比数列,由此能求出
an=atn-1.
(Ⅱ)当t=1时,S
n=an,b
n=an+1,当a>0时,不合题意;当a<0时,由题意知:b
4>0,b
6<0,且
,由此能求出a的取值范围.
(Ⅲ)
bn=1+,{c
n}为等比数列,从而
,由此能求出满足条件的数对是(1,2).
解答:
解:(Ⅰ)当n=1时,由S
2=tS
1+a,解得a
2=at,
当n≥2时,S
n=tS
n-1+a,
∴(S
n+1-S
n)=t(S
n-S
n-1),即a
n+1=ta
n又a
1=a≠0,综上有
=t(n∈N*),
即{a
n}是首项为a,公比为t的等比数列,
∴
an=atn-1.
(Ⅱ)当t=1时,S
n=an,b
n=an+1,
当a>0时,{b
n}单调递增,且b
n>0,不合题意;
当a<0时,{b
n}单调递减,由题意知:b
4>0,b
6<0,
且
解得
-≤a≤-,
综上a的取值范围为
[-,-].
(Ⅲ)∵t≠1,∴
bn=1+,
∴
cn=2+(1+)n-(t+t2+…+tn)=2+(1+)n-=
2-+(1+)n+由题设知{c
n}为等比数列,
∴
,
解得
,
即满足条件的数对是(1,2).
点评:本题考查数列{an}的通项公式的求法,考查a的取值范围的求法,考查能够使数列{cn}为等比数列的所有数(a,t)的求法,解题时要注意等差数列和等比数列的性质的合理运用.



 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案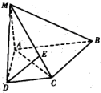 如图,在四棱锥M-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC-2,AB=4,MA=2,MA⊥平面ABCD.
如图,在四棱锥M-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC-2,AB=4,MA=2,MA⊥平面ABCD. 如图所示,在一个直角三角形的草地建一个长方形ABCD的体育场
如图所示,在一个直角三角形的草地建一个长方形ABCD的体育场