
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() 是边长为2的等边三角形,底面
是边长为2的等边三角形,底面![]() 是菱形,且
是菱形,且![]() .
.

![]() 证明:
证明:![]() ;
;
![]() 求平面
求平面![]() 与平面
与平面![]() 所成二面角的大小.
所成二面角的大小.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
![]() 取AD的中点E,连结PE,BE,BD,推导出
取AD的中点E,连结PE,BE,BD,推导出![]() ,
,![]() ,从而
,从而![]() 平面PBE,由此能证明
平面PBE,由此能证明![]() .
.
![]() ,EB,EP两两垂直,以E为坐标原点建立空间直角坐标系
,EB,EP两两垂直,以E为坐标原点建立空间直角坐标系![]() ,求出各点的坐标,再求出平面PBC的一个法向量
,求出各点的坐标,再求出平面PBC的一个法向量![]() 1,
1,![]() ,利用向量法即可求出平面PAD与平面PBC所成二面角的大小.
,利用向量法即可求出平面PAD与平面PBC所成二面角的大小.
证明:![]() 取AD的中点E,连结PE, BE,BD,
取AD的中点E,连结PE, BE,BD,
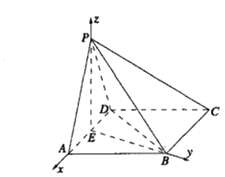
![]() 四边形ABCD是菱形,
四边形ABCD是菱形,![]() ,
,
![]() 是等边三角形,
是等边三角形,![]() ,
,
同理,得![]() ,
,
又![]() ,
,![]() 平面PBE,
平面PBE,![]() 平面PBE,
平面PBE,
![]() 平面PBE,
平面PBE,
又![]() 平面PBE,
平面PBE,![]() .
.
![]() 平面
平面![]() 平面ABCD,
平面ABCD,
由![]() 可知EA,EB,EP两两垂直,以E为坐标原点建立空间直角坐标系
可知EA,EB,EP两两垂直,以E为坐标原点建立空间直角坐标系![]() ,如图,
,如图,
由题意得![]() ,
,
则![]() 0,
0,![]() ,
,![]() ,
,![]() ,
,![]() 0,
0,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面PBC的一个法向量![]() y,
y,![]() ,
,
由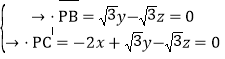 ,取
,取![]() ,得
,得![]() 1,
1,![]() ,
,
由![]() 得
得![]() 是平面PAD的一个法向量,
是平面PAD的一个法向量,
![]() ,
,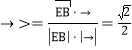 ,
,![]() ,
,
![]() 平面PAD与平面PBC所成二面角的大小为
平面PAD与平面PBC所成二面角的大小为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知曲线![]() 上的任意一点到两定点
上的任意一点到两定点![]() 、
、![]() 距离之和为
距离之和为![]() ,直线
,直线![]() 交曲线
交曲线![]() 于
于![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.
(1)求曲线![]() 的方程;
的方程;
(2)若![]() 不过点
不过点![]() 且不平行于坐标轴,记线段
且不平行于坐标轴,记线段![]() 的中点为
的中点为![]() ,求证:直线
,求证:直线![]() 的斜率与
的斜率与![]() 的斜率的乘积为定值;
的斜率的乘积为定值;
(3)若直线![]() 过点
过点![]() ,求
,求![]() 面积的最大值,以及取最大值时直线
面积的最大值,以及取最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足a1+a4=18,a2+a5=36.
(1)求数列{an}的通项公式an;
(2)若数列{bn}满足bn=an+log2an,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2lnx﹣2mx+x2(m>0).
(1)讨论函数f(x)的单调性;
(2)当![]() 时,若函数f(x)的导函数f′(x)的图象与x轴交于A,B两点,其横坐标分别为x1,x2(x1<x2),线段AB的中点的横坐标为x0,且x1,x2恰为函数h(x)=lnx﹣cx2﹣bx的零点.求证(x1﹣x2)h'(x0)≥
时,若函数f(x)的导函数f′(x)的图象与x轴交于A,B两点,其横坐标分别为x1,x2(x1<x2),线段AB的中点的横坐标为x0,且x1,x2恰为函数h(x)=lnx﹣cx2﹣bx的零点.求证(x1﹣x2)h'(x0)≥![]() +ln2.
+ln2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设非直角![]() 的内角
的内角![]() 、
、![]() 、
、![]() 所对边的长分别为
所对边的长分别为![]() 、
、![]() 、
、![]() ,则下列结论正确的是_____(写出所有正确结论的编号).
,则下列结论正确的是_____(写出所有正确结论的编号).
①“![]() ”是“
”是“![]() ”的充分必要条件
”的充分必要条件
②“![]() ”是“
”是“![]() ”的充分必要条件
”的充分必要条件
③“![]() ”是“
”是“![]() ”的充分必要条件
”的充分必要条件
④“![]() ”是“
”是“![]() ”的充分必要条件
”的充分必要条件
⑤“![]() ”是“
”是“![]() ”的充分必要条件
”的充分必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O是平面直角坐标系的原点,双曲线![]() .
.
(1)过双曲线![]() 的右焦点
的右焦点![]() 作x轴的垂线,交
作x轴的垂线,交![]() 于A、B两点,求线段AB的长;
于A、B两点,求线段AB的长;
(2)设M为![]() 的右顶点,P为
的右顶点,P为![]() 右支上任意一点,已知点T的坐标为
右支上任意一点,已知点T的坐标为![]() ,当
,当![]() 的最小值为
的最小值为![]() 时,求t的取值范围;
时,求t的取值范围;
(3)设直线![]() 与
与![]() 的右支交于A,B两点,若双曲线右支上存在点C使得
的右支交于A,B两点,若双曲线右支上存在点C使得![]() ,求实数m的值和点C的坐标.
,求实数m的值和点C的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
空气质量指数 |
|
|
|
|
|
|
空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
该社团将该校区在2018年11月中10天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.

(Ⅰ)以这10天的空气质量指数监测数据作为估计2018年11月的空气质量情况,则2018年11月中有多少天的空气质量达到优良?
(Ⅱ)已知空气质量等级为1级时不需要净化空气,空气质量等级为2级时每天需净化空气的费用为1000元,空气质量等量等级为3级时每天需净化空气的费用为2000元.若从这10天样本中空气质量为1级、2级、3级的天数中任意抽取两天,求这两天的净化空气总费用为3000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,我国某海岸线可看作由圆弧AB和射线BC连接而成,其中圆弧AB所在圆O的半径为12海里,圆心角为120°,规定外轮除特许外,不得进入离我国海岸线12海里以内的区域.在港口A处设有观察站,外轮一旦进入规定区域,观察站会接收到预警信号,现从A处测得一外轮在北偏东60°,距离港口x海里的P处,沿直线PA方向航行.
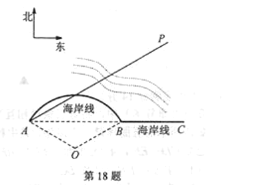
(1)当x=30时,分别求出外轮到海岸线BC和弧AB的最短距离,并判断观察站是否接收到预警信号?
(2)当x为何值时,观察站开始接收到预警信号?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com