
分析 (1)由f(x)≥0在[$\frac{1}{2}$,4]上恒成立,得到a≤x+$\frac{4}{x}$在[$\frac{1}{2}$,4]上恒成立,利用基本不等式求出右边的最小值,即可求a的取值范围;
(2)f(x)=3,a=x+$\frac{1}{x}$,结合基本不等式,利用方程f(x)=3在[$\frac{1}{2}$,4]上有两个解,求a的取值范围.
解答 解:(1)由f(x)≥0在[$\frac{1}{2}$,4]上恒成立,得到a≤x+$\frac{4}{x}$在[$\frac{1}{2}$,4]上恒成立,
∵x+$\frac{4}{x}$≥4,当且仅当x=2时取等号,
∴a≤4;
(2)f(x)=3,∴a=x+$\frac{1}{x}$,
由g(x)=x+$\frac{1}{x}$,在[$\frac{1}{2}$,1)上单调递减,(1,4]上单调递增,g($\frac{1}{2}$)=$\frac{5}{2}$,g(4)=$\frac{17}{4}$,g(1)=2,$\frac{17}{4}>\frac{5}{2}$,
∴方程f(x)=3在[$\frac{1}{2}$,4]上有两个解,a的取值范围是(2,$\frac{5}{2}$].
点评 本题考查恒成立问题,考查基本不等式的运用,正确转化是关键.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{5}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ?p∧?q | C. | ?p∧q | D. | p∧?q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
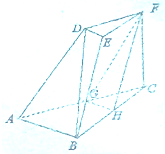 如图,三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.
如图,三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com