
分析 根据直线ax+by+1=0被圆x2+y2=25截得的弦长等于8建立关系,找出a,b的关系,利用基本不等式求解即可.
解答 解:圆x2+y2=25,其圆心为(0,0,),半径r=5,
圆心O到直线l的距离d=$\frac{1}{\sqrt{{a}^{2}+{b}^{2}}}$
弦长=2$\sqrt{{r}^{2}-{d}^{2}}$=8,
可得:${a}^{2}+{b}^{2}=\frac{1}{9}$,即9a2+9b2=1,
那么:($\frac{1}{{a}^{2}}$+$\frac{2}{{b}^{2}}$)(9a2+9b2)=9+18+$\frac{9{b}^{2}}{{a}^{2}}+\frac{18{a}^{2}}{{b}^{2}}$$≥27+2\sqrt{9×18}$=27+$18\sqrt{2}$
(当且仅当${b}^{2}=\sqrt{2}{a}^{2}$时取等号).
∴$\frac{1}{{a}^{2}}$+$\frac{2}{{b}^{2}}$的最小值等于27+$18\sqrt{2}$.
故答案为:27+$18\sqrt{2}$
点评 本题主要考查直线和圆的位置关系的弦长的运用,根据截得的弦长等于8建立关系,找出a,b的关系是解决本题的关键.属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 若a?α,b?α,c⊥a,c⊥b 则c⊥α | B. | 若a⊥α,b⊥α 则a∥b | ||
| C. | 若a∥α,α∩β=b 则a∥b | D. | 若b?α,a∥b 则 a∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 8 | C. | 4 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | [1,2) | C. | (2,5] | D. | [2,5] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -3 | C. | -2 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 32 | C. | 20 | D. | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
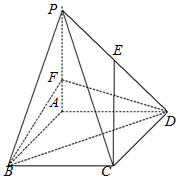 如图,在四棱锥 P-ABCD 中,底面 ABCD是菱形,PA⊥平面 ABCD,PA=3,F 是棱 PA 上的一个动点,E 为 PD 的中点.
如图,在四棱锥 P-ABCD 中,底面 ABCD是菱形,PA⊥平面 ABCD,PA=3,F 是棱 PA 上的一个动点,E 为 PD 的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,4) | B. | (4,-1) | C. | (4,1) | D. | (-1,4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com