
分析 (1)由抛物线的定义可得点P的轨迹C1为抛物线,再利用坐标变换得到曲线C2.
(2)设直线直线l1的斜率为k(k≠0),则l2的斜率为-$\frac{1}{k}$,其直线方程分别为:y=kx+1,y=-$\frac{1}{k}$x+1.设A(x1,y1),B(x2,y2),分别与抛物线方程联立可得A,B的坐标,利用就不不等式的性质及其S△AMB=$\frac{1}{2}|AM||BM|$,即可得出.
解答 解:(1)由抛物线的定义可得:点P的轨迹C1为抛物线:x2=y.
将曲线C1上每一点的横坐标变为原来的2倍,再向上平移1个单位得到曲线C2:$(\frac{1}{2}x)^{2}$=y-1,可得y=$\frac{1}{4}{x}^{2}$+1.
(2)设直线直线l1的斜率为k(k≠0),则l2的斜率为-$\frac{1}{k}$,其直线方程分别为:y=kx+1,y=-$\frac{1}{k}$x+1.设A(x1,y1),B(x2,y2),
联立$\left\{\begin{array}{l}{y=kx+1}\\{y=\frac{1}{4}{x}^{2}+1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$,$\left\{\begin{array}{l}{x=4k}\\{y=4{k}^{2}+1}\end{array}\right.$,可得A(4k,4k2+1).
同理可得B$(-\frac{4}{k},\frac{4}{{k}^{2}}+1)$.
∴S△AMB=$\frac{1}{2}|AM||BM|$=$\frac{1}{2}$$\sqrt{16{k}^{2}+(4{k}^{2}+1-1)^{2}}$$\sqrt{\frac{16}{{k}^{2}}+(\frac{4}{{k}^{2}}+1-1)^{2}}$=8$\sqrt{2+{k}^{2}+\frac{1}{{k}^{2}}}$≥8$\sqrt{2+2\sqrt{{k}^{2}•\frac{1}{{k}^{2}}}}$=16,当且仅当k=±1时取等号.
∴当k=±1时,△AMB的面积取得最小值16.
点评 本题考查了抛物线的标准方程及其性质、直线与抛物线相交弦长问题、两点之间距离公式、三角形面积计算公式、基本不等式的性质,考查了推理能力与计算能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
| 年份2007+x(年) | 0 | 1 | 2 | 3 | 4 |
| 人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2b-$\frac{4}{3}$ | B. | $\frac{3}{2}$b-$\frac{2}{3}$ | C. | 0 | D. | b2-$\frac{1}{6}$b3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
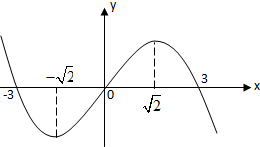
| A. | f(x)极大值为f($\sqrt{2}$),极小值为f(-$\sqrt{2}$) | B. | f(x)极大值为f(-$\sqrt{2}$),极小值为f($\sqrt{2}$) | ||
| C. | f(x)极大值为f(3),极小值为f(-3) | D. | f(x)极大值为f(-3),极小值为f(3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<$\frac{1}{e}$ | B. | a>$\frac{1}{e}$ | C. | a>$\frac{1}{2}$ | D. | a<$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com