
分析 (1)根据点P的坐标求得α的三角函数值,然后利用诱导公式对所求的代数式进行化简,并代入求值即可;
(2)分k为偶数和奇数两种情况,分别利用诱导公式进行化简求值.
解答 解:(1)∵角α终边上一点P(-4,3),
∴x=-4,y=3,r=|OP|=5,sin$α=\frac{y}{r}$=$\frac{3}{5}$,cos$α=\frac{x}{r}$=-$\frac{4}{5}$,
∴$\frac{{cos(\frac{π}{2}+α)sin(-π-α)}}{{cos(\frac{11π}{2}-α)sin(\frac{9π}{2}+α)}}$=$\frac{-sinαsinα}{-sinαcosα}$=$\frac{sinα}{cosα}$=-$\frac{3}{4}$.
(2)当k为偶数时,原式=$\frac{sin(kπ-α)cos[(k+1)π-α]}{sin[(k-1)π+α]cos(kπ+α)}$=$\frac{(-sinα)cosα}{sinαcosα}$=-1;
当k为奇数时,原式=$\frac{sin(kπ-α)cos[(k+1)π-α]}{sin[(k-1)π+α]cos(kπ+α)}$=$\frac{sinα(-cosα)}{(-sinα)(-cosα)}$=-1;
综上可得,$\frac{sin(kπ-α)cos[(k+1)π-α]}{sin[(k-1)π+α]cos(kπ+α)}$=-1.
点评 本题主要考查了诱导公式在三角函数化简求值中的应用,考查了分类讨论思想,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
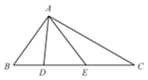 在△ABC中,D、E是BC边上两点,BD、BA、BC构成以2为公比的等比数列,BD=6,∠AEB=2∠BAD,AE=9,则三角形ADE的面积为( )
在△ABC中,D、E是BC边上两点,BD、BA、BC构成以2为公比的等比数列,BD=6,∠AEB=2∠BAD,AE=9,则三角形ADE的面积为( )| A. | 31.2 | B. | 32.4 | C. | 33.6 | D. | 34.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | $\frac{21}{2}$ | D. | $\frac{33}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>1} | B. | {x|x>0} | C. | {x|0<x<2} | D. | {x|1<x<2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com