
 ij����ʱ���շѣ��շѱ�Ϊ��ÿ��һ�β�����1Сʱ�շ�10Ԫ������1Сʱ�IJ���ÿСʱ�շ�8Ԫ������1Сʱ�IJ��ְ�1Сʱ���㣩�����мס��Ҷ��˲��뵫��������4Сʱ���ס��Ҷ�����ÿ��ʱ���볡�ǵȿ��ܵģ�Ϊ�����˿ͣ�ÿ���˿Ϳ��Բμ�һ�γ齱���
ij����ʱ���շѣ��շѱ�Ϊ��ÿ��һ�β�����1Сʱ�շ�10Ԫ������1Сʱ�IJ���ÿСʱ�շ�8Ԫ������1Сʱ�IJ��ְ�1Сʱ���㣩�����мס��Ҷ��˲��뵫��������4Сʱ���ס��Ҷ�����ÿ��ʱ���볡�ǵȿ��ܵģ�Ϊ�����˿ͣ�ÿ���˿Ϳ��Բμ�һ�γ齱������� ��1�������aԪ���Ҹ���bԪ������a��b=10��18��26��34���ɴ������оٷ���������ס��Ҷ��˸���֮��Ϊ44Ԫ���ĸ��ʣ�
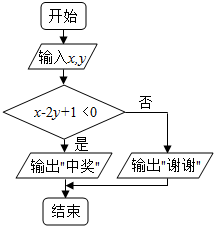
��2������֪0��x��1��0��y��1�㣨x��y����������OABC�ڣ���������$\left\{\begin{array}{l}x-2y+1��0\\ 0��x��1\\ 0��y��1\end{array}\right.$�������ɴ�������˿��н��ĸ��ʣ�
��� 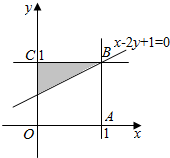 �⣺��1�������aԪ���Ҹ���bԪ������a��b=10��18��26��34��
�⣺��1�������aԪ���Ҹ���bԪ������a��b=10��18��26��34��
��ס��Ҷ��˵ķ��ù��ɵĻ����¼��ռ�Ϊ��
��10��10������10��18������10��26������10��34������18��10������18��18������18��26������18��34����
��26��10������26��18������26��26������26��34������34��10������34��18������34��26������34��34����16�����Σ���4�֣�
���У���10��34������18��26������26��18������34��10����4�����η������⣮
�ʡ��ס��Ҷ��˸���֮��Ϊ44Ԫ���ĸ���Ϊ$P=\frac{4}{16}=\frac{1}{4}$����6�֣�
��2������֪0��x��1��0��y��1�㣨x��y����ͼ��������OABC�ڣ�
������$\left\{\begin{array}{l}x-2y+1��0\\ 0��x��1\\ 0��y��1\end{array}\right.$���õ�������Ϊͼ����Ӱ���֣���9�֣�
��x-2y+1=0����x=0��$y=\frac{1}{2}$����x=1��y=1��
������������������$s=\frac{1}{2}��\frac{1}{2}��1=\frac{1}{4}$����11�֣�
��˿��н����¼�ΪN����˿��н��ĸ���$p��N��=\frac{{\frac{1}{4}}}{1}=\frac{1}{4}$����12�֣�
���� ���⿼����ʵ����ǻ����⣬����ʱҪ�������⣬ע���оٷ��ͼ��θ��͵ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
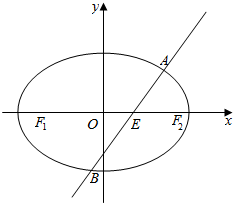 ��ͼ����ƽ��ֱ������ϵxOy�У���ԲC��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{2}}{2}$��ֱ��l��x�ύ�ڵ�E������ԲC����A��B���㣮��ֱ��l��ֱ��x���ҵ�EΪ��ԲC���ҽ���ʱ����AB�ij�Ϊ$\sqrt{2}$��
��ͼ����ƽ��ֱ������ϵxOy�У���ԲC��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{2}}{2}$��ֱ��l��x�ύ�ڵ�E������ԲC����A��B���㣮��ֱ��l��ֱ��x���ҵ�EΪ��ԲC���ҽ���ʱ����AB�ij�Ϊ$\sqrt{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��p��q���� | B�� | ��p��q���� | C�� | ���Vq���� | D�� | ��p��q���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | $2\sqrt{2}$ | C�� | $3\sqrt{2}$ | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��1��ִ����ͼ��ʾ�ij����ͼ����������t��[-1��3]���������s��ȡֵ��Χ��Ϊ����A����A��
��1��ִ����ͼ��ʾ�ij����ͼ����������t��[-1��3]���������s��ȡֵ��Χ��Ϊ����A����A���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com