
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:解答题
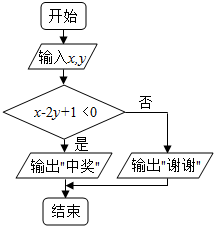 某乐园按时段收费,收费标准为:每玩一次不超过1小时收费10元,超过1小时的部分每小时收费8元(不足1小时的部分按1小时计算).现有甲、乙二人参与但都不超过4小时,甲、乙二人在每个时段离场是等可能的.为吸引顾客,每个顾客可以参加一次抽奖活动.
某乐园按时段收费,收费标准为:每玩一次不超过1小时收费10元,超过1小时的部分每小时收费8元(不足1小时的部分按1小时计算).现有甲、乙二人参与但都不超过4小时,甲、乙二人在每个时段离场是等可能的.为吸引顾客,每个顾客可以参加一次抽奖活动.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{7}{9}$ | B. | $\frac{7}{9}$ | C. | $-\frac{8}{9}$ | D. | $\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
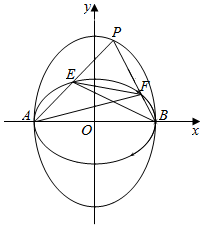 椭圆C1与C2的中心在原点,焦点分别在x轴与y轴上,它们有相同的离心率$e=\frac{{\sqrt{2}}}{2}$,并且C2的短轴为C1的长轴,C1与C2的四个焦点构成的四边形面积是$2\sqrt{2}$.
椭圆C1与C2的中心在原点,焦点分别在x轴与y轴上,它们有相同的离心率$e=\frac{{\sqrt{2}}}{2}$,并且C2的短轴为C1的长轴,C1与C2的四个焦点构成的四边形面积是$2\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)是最小正周期为π的奇函数 | B. | f(x)是最小正周期为π的偶函数 | ||
| C. | f(x)是最小正周期为$\frac{π}{2}$的偶函数 | D. | f(x)是最小正周期为$\frac{π}{2}$的奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}+\frac{y^2}{9}=1$ | B. | $\frac{x^2}{64}+\frac{y^2}{57}=1$ | C. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | D. | $\frac{x^2}{64}-\frac{y^2}{57}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com