
| A. | $\frac{x^2}{16}+\frac{y^2}{9}=1$ | B. | $\frac{x^2}{64}+\frac{y^2}{57}=1$ | C. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | D. | $\frac{x^2}{64}-\frac{y^2}{57}=1$ |
分析 由已知得Q为PN的中点且GQ⊥PN,|GN|+|GM|=|MP|=8,从而得到G点的轨迹是以M、N为焦点的椭圆,其长半轴长a=4,半焦距c=$\sqrt{7}$,由此能求出点G的轨迹方程.
解答 解:∵圆$M:{(x+\sqrt{7})^2}+{y^2}=64$,定点$N(\sqrt{7},0)$,点P为圆M上的动点,
∴M(-$\sqrt{7}$,0),PM=8,
∵点Q在NP上,$点G在线段MP上,且满足\overrightarrow{NP}=2\overrightarrow{NQ}$,$\overrightarrow{GQ}•\overrightarrow{NP}$=0,
∴Q为PN的中点且GQ⊥PN,∴GQ为PN的中垂线,
∴|PG|=|GN|,∴|GN|+|GM|=|MP|=8,
故G点的轨迹是以M、N为焦点的椭圆,其长半轴长a=4,半焦距c=$\sqrt{7}$,
∴短半轴长b=$\sqrt{16-7}$=3,
∴点G的轨迹方程是$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{9}$=1.
故选:A.
点评 本题考查点的轨迹方程的求法,是中档题,解题时要认真审题,注意椭圆定义和性质的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 (1)执行如图所示的程序框图,如果输入的t∈[-1,3],若输出的s的取值范围记为集合A,求集合A;
(1)执行如图所示的程序框图,如果输入的t∈[-1,3],若输出的s的取值范围记为集合A,求集合A;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
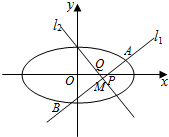 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(0,1),离心率为 $\frac{\sqrt{3}}{2}$,点O为坐标原点.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(0,1),离心率为 $\frac{\sqrt{3}}{2}$,点O为坐标原点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | -1 | C. | 2 | D. | -1或2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
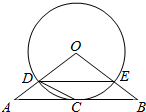 如图,△ABO三边上的点C、D、E都在⊙O上,已知AB∥DE,AC=CB.
如图,△ABO三边上的点C、D、E都在⊙O上,已知AB∥DE,AC=CB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
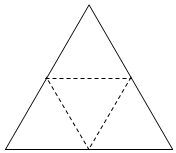 如图所示的平面图形是边长为8的正三角形,沿三边中点连线向同一方向折成一个多面体.
如图所示的平面图形是边长为8的正三角形,沿三边中点连线向同一方向折成一个多面体.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com