
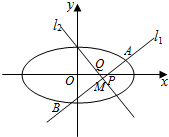
 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(0,1),离心率为 $\frac{\sqrt{3}}{2}$,点O为坐标原点.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(0,1),离心率为 $\frac{\sqrt{3}}{2}$,点O为坐标原点.分析 (Ⅰ)由已知得b=1,e=$\frac{c}{a}=\frac{\sqrt{3}}{2}$,由此能求出椭圆E的标准方程.
(Ⅱ)(i)将直线y=kx+m代入$\frac{{x}^{2}}{4}+{y}^{2}=1$,得(1+4k2)x2+8kmx+4m2-4=0,由此利用韦达定理、斜率公式能证明直线OM的斜率与直线l1的斜率之积为定值.
(ii)当m=-k时,直线l1:y=k(x-1),P(1,0),从而M($\frac{4{k}^{2}}{1+4{k}^{2}}$,$\frac{-k}{1+4{k}^{2}}$),直线l2方程为y-$\frac{-k}{1+4{k}^{2}}$=-$\frac{1}{k}(x-\frac{4{k}^{2}}{1+4{k}^{2}})$,从而|PQ|=$\frac{1+{k}^{2}}{1+4{k}^{2}}$,由此利用弦长公式能求出$\frac{|AB|}{|PQ|}$的取值范围.
解答 解:(Ⅰ)∵椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(0,1),离心率为 $\frac{\sqrt{3}}{2}$,点O为坐标原点,
∴b=1,e=$\frac{c}{a}=\frac{\sqrt{3}}{2}$,∴$\frac{{c}^{2}}{{a}^{2}}=\frac{{a}^{2}-1}{{a}^{2}}=\frac{3}{4}$,
解得a2=4,
∴椭圆E的标准方程为$\frac{{x}^{2}}{{4}^{\;}}$+y2=1.
证明:(Ⅱ)(i)将直线y=kx+m代入$\frac{{x}^{2}}{4}+{y}^{2}=1$,整理,得(1+4k2)x2+8kmx+4m2-4=0,
设A(x1,y1),B(x2,y2),则${x}_{1}+{x}_{2}=-\frac{8km}{1+4{k}^{2}}$,${x}_{1}{x}_{2}=\frac{4{m}^{2}-4}{1+4{k}^{2}}$,
∴${x}_{0}=-\frac{4km}{1+4{k}^{2}}$,${y}_{0}=k{x}_{0}+m=\frac{m}{1+4{k}^{2}}$,
∴M(-$\frac{4km}{1+4{k}^{2}}$,$\frac{m}{1+4{k}^{2}}$),
∴${k}_{OM}•{k}_{{l}_{1}}$=$\frac{\frac{m}{1+4{k}^{2}}}{-\frac{4km}{1+4{k}^{2}}}$•k=-$\frac{1}{4k}•k=-\frac{1}{4}$.
解:(ii)当m=-k时,由(i)知直线l1:y=k(x-1),∴P(1,0),
∴${x}_{1}+{x}_{2}=\frac{8{k}^{2}}{1+4{k}^{2}}$,${x}_{1}{x}_{2}=\frac{4{k}^{2}-4}{1+4{k}^{2}}$,
∴M($\frac{4{k}^{2}}{1+4{k}^{2}}$,$\frac{-k}{1+4{k}^{2}}$),
∴直线l2方程为y-$\frac{-k}{1+4{k}^{2}}$=-$\frac{1}{k}(x-\frac{4{k}^{2}}{1+4{k}^{2}})$,
令y=0,得x=$\frac{3{k}^{2}}{1+4{k}^{2}}$,∴Q($\frac{3{k}^{2}}{1+4{k}^{2}}$,0),
∴|PQ|=|1-$\frac{3{k}^{2}}{1+4{k}^{2}}$|=$\frac{1+{k}^{2}}{1+4{k}^{2}}$,
又|AB|=$\sqrt{1+{k}^{2}}$|x2-x1|=$\sqrt{1+{k}^{2}}$$\sqrt{(\frac{8{k}^{2}}{1+4{k}^{2}})^{2}-4•\frac{4{k}^{2}-4}{1+4{k}^{2}}}$
=$\frac{4\sqrt{(1+{k}^{2})(1+3{k}^{2})}}{1+4{k}^{2}}$,
∴$\frac{|AB|}{|PQ|}$=$\frac{\frac{4\sqrt{(1+{k}^{2})(1+3{k}^{2})}}{1+4{k}^{2}}}{\frac{1+{k}^{2}}{1+4{k}^{2}}}$=4$\sqrt{\frac{1+3{k}^{2}}{1+{k}^{2}}}$=4$\sqrt{3-\frac{2}{1+{k}^{2}}}$,
∵k≠0,∴1<3-$\frac{2}{1+{k}^{2}}$<3,
∴$\frac{|AB|}{|PQ|}$的取值范围是(4,4$\sqrt{3}$).
点评 本题考查椭圆方程的求法,考查两直线的斜率之积为定值的证明,考查两线段比值的取值范围的求法,是中档题,解题时要认真审题,注意弦长公式的合理运用.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:解答题
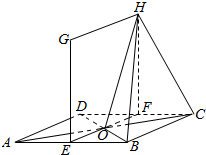 如图,菱形ABCD中,∠BAD=60°,边长AB=2,GE⊥平面ABCD,EF⊥ABCD,E,F分别是边AB、CD中点,AC与BD交于O,EG=FH=2,
如图,菱形ABCD中,∠BAD=60°,边长AB=2,GE⊥平面ABCD,EF⊥ABCD,E,F分别是边AB、CD中点,AC与BD交于O,EG=FH=2,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{7}{9}$ | B. | $\frac{7}{9}$ | C. | $-\frac{8}{9}$ | D. | $\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b2 | B. | ab | C. | ac | D. | bc |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
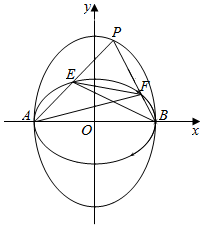 椭圆C1与C2的中心在原点,焦点分别在x轴与y轴上,它们有相同的离心率$e=\frac{{\sqrt{2}}}{2}$,并且C2的短轴为C1的长轴,C1与C2的四个焦点构成的四边形面积是$2\sqrt{2}$.
椭圆C1与C2的中心在原点,焦点分别在x轴与y轴上,它们有相同的离心率$e=\frac{{\sqrt{2}}}{2}$,并且C2的短轴为C1的长轴,C1与C2的四个焦点构成的四边形面积是$2\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)是最小正周期为π的奇函数 | B. | f(x)是最小正周期为π的偶函数 | ||
| C. | f(x)是最小正周期为$\frac{π}{2}$的偶函数 | D. | f(x)是最小正周期为$\frac{π}{2}$的奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}+\frac{y^2}{9}=1$ | B. | $\frac{x^2}{64}+\frac{y^2}{57}=1$ | C. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | D. | $\frac{x^2}{64}-\frac{y^2}{57}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com