
分析 (1)当a=1时,求出函数f(x)的表达式,判断函数的单调性即可求f(x)的最小值;
(2)当f(x)有最小值时,利用分段函数的性质建立不等式关系即可求a的取值范围;
(3)利用换元法,结合函数与方程之间的关系进行转化,求a的取值范围.
解答 解:(1)当a=1时,f(x)=2|x-2|+x=$\left\{\begin{array}{l}{3x-4,}&{x≥2}\\{-x+4,}&{x<2}\end{array}\right.$…(2分)
所以,f(x)在(-∞,2)递减,在[2,+∞)递增,
故最小值为f(2)=2; …(4分)
(2)f(x)=$\left\{\begin{array}{l}{(a+2)x-4,}&{x≥2}\\{(a-2)x+4,}&{x<2}\end{array}\right.$,…(6分)
要使函数f(x)有最小值,需$\left\{\begin{array}{l}{a+2≥0}\\{a-2≤0}\end{array}\right.$,
∴-2≤a≤2,…(8分)
故a的取值范围为[-2,2]. …(9分)
(3)∵sinx∈[-1,1],∴f(sinx)=(a-2)sinx+4,
“h(x)=f(sinx)-2=(a-2)sinx+2存在零点”等价于“方程(a-2)sinx+2=0有解”,
亦即$sinx=-\frac{2}{a-2}$有解,
∴$-1≤-\frac{2}{a-2}≤1$,…(11分)
解得a≤0或a≥4,…(13分)
∴a的取值范围为(-∞,0]∪[4,+∞)…(14分)
点评 本题主要考查分段函数的应用,利用分段函数的表达式结合一元二次函数的性质,是解决本题的关键.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “p∨q”假 | B. | “p∧q”真 | C. | “¬q”真 | D. | “p∨q”真 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 (1)执行如图所示的程序框图,如果输入的t∈[-1,3],若输出的s的取值范围记为集合A,求集合A;
(1)执行如图所示的程序框图,如果输入的t∈[-1,3],若输出的s的取值范围记为集合A,求集合A;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<1<b | B. | a<b<1 | C. | 1<a<b | D. | b<1<a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (1,+∞) | C. | (1,2)∪(2,+∞) | D. | (1,3)∪(3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
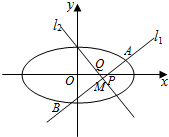 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(0,1),离心率为 $\frac{\sqrt{3}}{2}$,点O为坐标原点.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(0,1),离心率为 $\frac{\sqrt{3}}{2}$,点O为坐标原点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com