
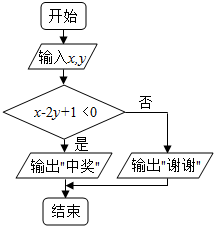
 (1)执行如图所示的程序框图,如果输入的t∈[-1,3],若输出的s的取值范围记为集合A,求集合A;
(1)执行如图所示的程序框图,如果输入的t∈[-1,3],若输出的s的取值范围记为集合A,求集合A;分析 (1)由程序框图可知,分段函数的对称轴为t=2,在[1,2]上单调递增,在[2,3]上单调递减,解得smax=3,smin=2,即可解得集合A.
(2)函数$f(x)=\frac{1}{3}{x^3}+a{x^2}+x+a$有极值,等价于f′(x)=x2+2ax+1=0有两个不相等的实数根,即△=(2a)2-4>0,由此能求出命题p:a<-1或a>1,利用p∧q为真命题,建立不等式组,即可解得实数a的取值范围.
解答 (本题满分为12分)
解:(1)由程序框图可知,当-1≤t<1时,s=2t,则s∈[-2,2),
当1≤t≤3时,s=-(t-2)2+3,
∵该函数的对称轴为t=2,
∴该函数在[1,2]上单调递增,在[2,3]上单调递减.
∴smax=3,smin=2,
∴s∈[2,3].
综上知,s∈[-2,3],集合A=[-2,3].…(4分)
(2)∵函数$f(x)=\frac{1}{3}{x^3}+a{x^2}+x+a$有极值,且f′(x)=x2+2ax+1,
∴f′(x)=0有两个不相等的实数根,即△=(2a)2-4>0,解得a<-1或a>1,
即命题p:a<-1或a>1.…(8分)
∵p∧q为真命题,
∴则$\left\{\begin{array}{l}{a<-1或a>1}\\{-2≤a≤3}\end{array}\right.$,解得-2≤a<-1或1<a≤3;
∴实数a的取值范围是[-2,-1)∪(1,3].…(12分)
点评 本题主要考查了选择结构的程序框图,考查函数的极大值和极小值的求法,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意导数性质的合理运用.


科目:高中数学 来源: 题型:解答题
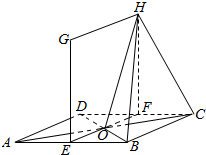 如图,菱形ABCD中,∠BAD=60°,边长AB=2,GE⊥平面ABCD,EF⊥ABCD,E,F分别是边AB、CD中点,AC与BD交于O,EG=FH=2,
如图,菱形ABCD中,∠BAD=60°,边长AB=2,GE⊥平面ABCD,EF⊥ABCD,E,F分别是边AB、CD中点,AC与BD交于O,EG=FH=2,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某乐园按时段收费,收费标准为:每玩一次不超过1小时收费10元,超过1小时的部分每小时收费8元(不足1小时的部分按1小时计算).现有甲、乙二人参与但都不超过4小时,甲、乙二人在每个时段离场是等可能的.为吸引顾客,每个顾客可以参加一次抽奖活动.
某乐园按时段收费,收费标准为:每玩一次不超过1小时收费10元,超过1小时的部分每小时收费8元(不足1小时的部分按1小时计算).现有甲、乙二人参与但都不超过4小时,甲、乙二人在每个时段离场是等可能的.为吸引顾客,每个顾客可以参加一次抽奖活动.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [3,+∞) | B. | (3,+∞) | C. | [-∞,3] | D. | [-∞,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{7}{9}$ | B. | $\frac{7}{9}$ | C. | $-\frac{8}{9}$ | D. | $\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}+\frac{y^2}{9}=1$ | B. | $\frac{x^2}{64}+\frac{y^2}{57}=1$ | C. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | D. | $\frac{x^2}{64}-\frac{y^2}{57}=1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com