
| A. | 2 | B. | $2\sqrt{2}$ | C. | $3\sqrt{2}$ | D. | 8 |
分析 先确定抛物线的焦点坐标,可得直线l的方程,与抛物线方程联立,求弦AB的长,再求出原点到直线的距离,即可求得△OAB的面积.
解答 解:抛物线C:y2=4x的焦点F(1,0),
∵直线l:y=x+b经过抛物线的焦点,
∴b=-1,
∴直线l:y=x-1,
由抛物线的定义:|AB|=xA+xB+2,
将直线与抛物线方程联立,消去y可得x2-6x+1=0,
∴xA+xB=6,
∴|AB|=8,
∵原点到直线的距离为d=$\frac{1}{\sqrt{2}}$,
∴S=$\frac{1}{2}×8×\frac{1}{\sqrt{2}}$=2$\sqrt{2}$.
故选:B.
点评 本题考查三角形面积的计算,考查直线与抛物线的位置关系,解题的关键是求出弦AB的长.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:解答题
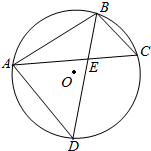 如图,圆O为△ABC的外接圆,D为$\widehat{AC}$的中点,BD交AC于E.
如图,圆O为△ABC的外接圆,D为$\widehat{AC}$的中点,BD交AC于E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 25 | C. | 10 | D. | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
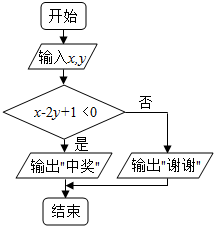 某乐园按时段收费,收费标准为:每玩一次不超过1小时收费10元,超过1小时的部分每小时收费8元(不足1小时的部分按1小时计算).现有甲、乙二人参与但都不超过4小时,甲、乙二人在每个时段离场是等可能的.为吸引顾客,每个顾客可以参加一次抽奖活动.
某乐园按时段收费,收费标准为:每玩一次不超过1小时收费10元,超过1小时的部分每小时收费8元(不足1小时的部分按1小时计算).现有甲、乙二人参与但都不超过4小时,甲、乙二人在每个时段离场是等可能的.为吸引顾客,每个顾客可以参加一次抽奖活动.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [3,+∞) | B. | (3,+∞) | C. | [-∞,3] | D. | [-∞,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $-\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $-\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com