Question

3．已知实数x，y满足x²+y²=3，则$\frac{y}{{x-2\sqrt{3}}}$的取值范围为[-$\frac{\sqrt{3}}{3}$，$\frac{\sqrt{3}}{3}$]．

Answer 1

分析 画出满足条件的平面区域，根据$\frac{y}{{x-2\sqrt{3}}}$的几何意义结合图象求出其范围即可．

解答 解：画出满足条件的平面区域，如图示：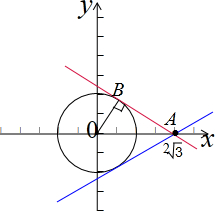
，
而$\frac{y}{{x-2\sqrt{3}}}$的几何意义表示过A（2$\sqrt{3}$，0）与圆上的点的直线的斜率，
显然直线与圆在上方与圆相切时，斜率最小，在下方与圆相切时，斜率最大，
由OA=2$\sqrt{3}$，OB=$\sqrt{3}$，得∠OAB=30°，∴直线AB的斜率是-$\frac{\sqrt{3}}{3}$，
同理可求：直线在圆的下方时即蓝色直线的斜率是：$\frac{\sqrt{3}}{3}$
故答案为：$[{-\frac{{\sqrt{3}}}{3}，\frac{{\sqrt{3}}}{3}}]$．

点评 本题考查了$\frac{y}{{x-2\sqrt{3}}}$的几何意义，考查数形结合思想，考查直线斜率公式，是一道基础题．