Question

20．已知圆M：（x-1）²+y²=$\frac{3}{8}$，椭圆C：$\frac{{x}^{2}}{3}$+y²=1，若直线l与椭圆交于A，B两点，与圆M相切于点P，且P为AB的中点，则这样的直线l有（　　）

• A． 2条
• B． 3条
• C． 4条
• D． 6条

Answer 1

分析 讨论直线AB的斜率不存在和存在，利用点差法求得直线AB的斜率，根据k_MP•k_AB=-1，求得P点横坐标，确定在椭圆内，即可得到所求直线的条数．

解答 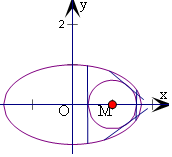解：当直线AB斜率不存在时且与圆M相切时，P在x轴上，
故满足条件的直线有两条；
当直线AB斜率存在时，设A（x₁，y₁），B（x₂，y₂），P（x₀，y₀），
由$\frac{{{x}_{1}}^{2}}{3}$+y₁²=1，$\frac{{{x}_{2}}^{2}}{3}$+y₂²=1，
两式相减，整理得：$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{1}{3}$•$\frac{{x}_{1}+{x}_{2}}{{y}_{1}+{y}_{2}}$，
则k_AB=-$\frac{{x}_{0}}{3{y}_{0}}$，k_MP=$\frac{{y}_{0}}{{x}_{0}-1}$，k_MP•k_AB=-1，
则k_MP•k_AB=-$\frac{{x}_{0}}{3{y}_{0}}$•$\frac{{y}_{0}}{{x}_{0}-1}$=-1，解得：x₀=$\frac{3}{2}$，
由$\frac{3}{2}$＜$\sqrt{3}$，可得P在椭圆内部，
则这样的P点有两个，即直线AB斜率存在时，也有两条．
综上可得，所求直线l有4条．
故选：C．

点评 本题考查点差法的应用，直线的斜率公式、中点坐标公式以及两直线垂直的条件，考查分类讨论和计算能力，属于中档题．