Question

已知函数f（x）=ax³+cx+d（a≠0）是R上的奇函数，当x=1时，f（x）取得极值-2．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）求f（x）的单调区间；
（Ⅲ）求f（x）在区间[-3，3]上的最大值与最小值．

Answer 1

分析：（1）由题中条件：“R上的奇函数”，得d=0，利用导数列出方程，即可求得参数得函数解析式；
（2）由f'（x）=3x²-3求得零点，利用导数的知识求得原函数的单调区间；
（3）欲求函数的最大值与最小值，通过列表格的方法研究原函数的单调性及在端点处和极值处的函数值的大小．

解答：解：（Ⅰ）由f（x）是R上的奇函数，有f（-x）=-f（x），（1分）
即-ax³-cx+d=-ax³-cx-d，所以d=0．
因此f（x）=ax³+cx．（2分）
对函数f（x）求导数，得f'（x）=3ax²+c．（3分）
由题意得f（1）=-2，f'（1）=0，（4分）
所以

a+c=-2 3a+c=0.

（5分）
解得a=1，c=-3，
因此f（x）=x³-3x．（6分）

（Ⅱ）f'（x）=3x²-3．（7分）
令3x²-3＞0，解得x＜-1或x＞1，
因此，当x∈（-∞，-1）时，f（x）是增函数；当x∈（1，+∞）时，f（x）也是增函数．（8分）
再令3x²-3＜0，解得-1＜x＜1．
因此，当x∈（-1，1）时，f（x）是减函数．（9分）

（Ⅲ）令f'（x）=0，得x₁=-1或x₂=1．
当x变化时，f'（x）、f（x）的变化如下表．

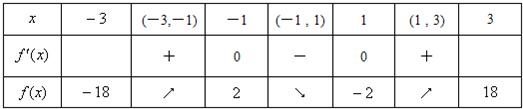
从上表可知，f（x）在区间[-3，3]上的最大值是18，最小值是-18．（13分）

点评：本题考查了函数的单调性，利用导数判断函数的单调性的步骤是：（1）确定函数的定义域；（2）求导数fˊ（x）；（3）在函数的定义域内解不等式fˊ（x）＞0和fˊ（x）＜0；（4）确定函数的单调区间．若在函数式中含字母系数，往往要分类讨论．