
已知函数f(x)=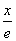 +
+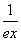 (e≈2.718…).
(e≈2.718…).
(1)若x1,x2∈[1,+∞),x1≠x2,求证: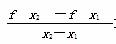 >0;
>0;
(2)若满足f(|a|+3)>f(|a-4|+1),试求实数a的取值范围.
科目:高中数学 来源: 题型:
在四边形ABCD中,“∃λ∈R,使得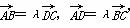 ”是“四边形ABCD为平行四边形”的( )
”是“四边形ABCD为平行四边形”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
已知a2sin θ+acos θ-2=0,b2sin θ+bcos θ-2=0(a,b,θ∈R,且a≠b),直线l过点A(a,a2),B(b,b2),则直线l被圆(x-cos θ)2+(y-sin θ)2=4所截得的弦长为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径.
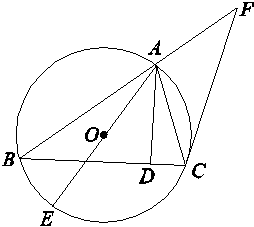
(1)求证:AC·BC=AD·AE;
(2)过点C作⊙O的切线交BA的延长线于点F,若AF=4,CF=6,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com