
如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径.
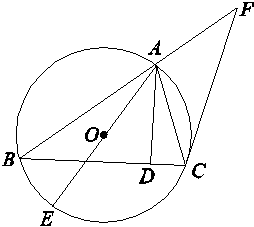
(1)求证:AC·BC=AD·AE;
(2)过点C作⊙O的切线交BA的延长线于点F,若AF=4,CF=6,求AC的长.
科目:高中数学 来源: 题型:
数列{an}的前n项和为Sn,且Sn=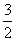 (an-1),数列{bn}满足bn=
(an-1),数列{bn}满足bn=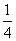 bn-1-
bn-1- (n≥2),且b1=3.
(n≥2),且b1=3.
(1)求数列{an}与{bn}的通项公式;
(2)设数列{cn}满足cn=an·log2(bn+1),其前n项和为Tn,求Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=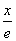 +
+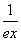 (e≈2.718…).
(e≈2.718…).
(1)若x1,x2∈[1,+∞),x1≠x2,求证: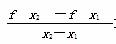 >0;
>0;
(2)若满足f(|a|+3)>f(|a-4|+1),试求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
设m,n是两条不同的直线,α,β,γ是三个不同的平面,有以下四个命题:
①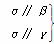 ⇒β∥γ ②
⇒β∥γ ②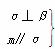 ⇒m⊥β ③
⇒m⊥β ③ ⇒α⊥β ④
⇒α⊥β ④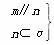 ⇒m∥α
⇒m∥α
其中正确的命题是( )
A.①④ B.②③
C.①③ D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com