
数列{an}的前n项和为Sn,且Sn=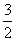 (an-1),数列{bn}满足bn=
(an-1),数列{bn}满足bn=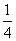 bn-1-
bn-1- (n≥2),且b1=3.
(n≥2),且b1=3.
(1)求数列{an}与{bn}的通项公式;
(2)设数列{cn}满足cn=an·log2(bn+1),其前n项和为Tn,求Tn.
解析:(1)对于数列{an}有Sn=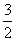 (an-1),①
(an-1),①
Sn-1=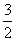 (an-1-1)(n≥2),②
(an-1-1)(n≥2),②
由①-②,得an=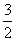 (an-an-1),即an=3an-1,
(an-an-1),即an=3an-1,
n=1时,S1=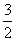 (a1-1)=a1,解得a1=3,
(a1-1)=a1,解得a1=3,
则an=a1·qn-1=3·3n-1=3n.
对于数列{bn},有bn=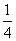 bn-1-
bn-1- (n≥2),
(n≥2),
可得bn+1=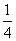 bn-1+
bn-1+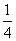 ,即
,即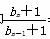 =
=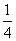 .
.
bn+1=(b1+1)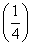 n-1=4
n-1=4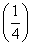 n-1=42-n,
n-1=42-n,
即bn=42-n-1.
(2)由(1)可知
cn=an·log2(bn+1)=3n·log2 42-n
=3n·log2 24-2n=3n(4-2n).
Tn=2·31+0·32+(-2)·33+…+(4-2n)·3n,③
3Tn=2·32+0·33+…+(6-2n)·3n+(4-2n)·3n+1,④
由③-④,得
-2Tn=2·3+(-2)·32+(-2)·33+…+(-2)·3n-(4-2n)·3n+1
=6+(-2)(32+33+…+3n)-(4-2n)·3n+1,
则Tn=-3+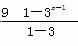 +(2-n)·3n+1
+(2-n)·3n+1
=-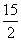 +
+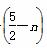 ·3n+1.
·3n+1.


科目:高中数学 来源: 题型:
如图,正三角形PAD所在平面与正方形ABCD所在平面互相垂直,O为正方形ABCD的中心,M为正方形ABCD内一点,且满足MP=MB,则点M的轨迹为( )
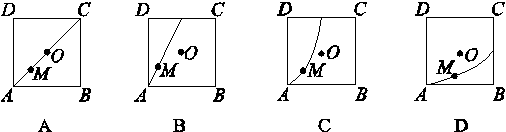
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在三棱锥O-ABC中,三条棱OA,OB,OC两两垂直,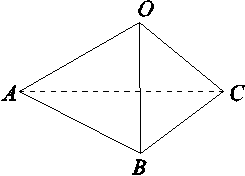
且OA>OB>OC,分别经过三条棱OA,OB,OC作一个截面平分三棱锥的体积,截面面积依次为S1,S2,S3,则S1,S2,S3的大小关系为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数y=Asin(ωx+φ)+k(A>0)的最大值为4,最小值为0,最小正周期为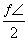 ,直线x=
,直线x=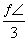 是其图象的一条对称轴,则下面各式中符合条件的解析式为( )
是其图象的一条对称轴,则下面各式中符合条件的解析式为( )
A.y=4sin B.y=2sin
B.y=2sin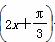 +2
+2
C.y=2sin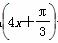 +2 D.y=2sin
+2 D.y=2sin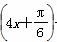 +2
+2
查看答案和解析>>
科目:高中数学 来源: 题型:
已知a2sin θ+acos θ-2=0,b2sin θ+bcos θ-2=0(a,b,θ∈R,且a≠b),直线l过点A(a,a2),B(b,b2),则直线l被圆(x-cos θ)2+(y-sin θ)2=4所截得的弦长为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径.
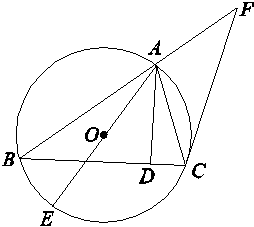
(1)求证:AC·BC=AD·AE;
(2)过点C作⊙O的切线交BA的延长线于点F,若AF=4,CF=6,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com